WHUCTF2025 WP

WP

MISC

[签到]益智游戏

1.数独

数独还没做完，直接爆破就出了。

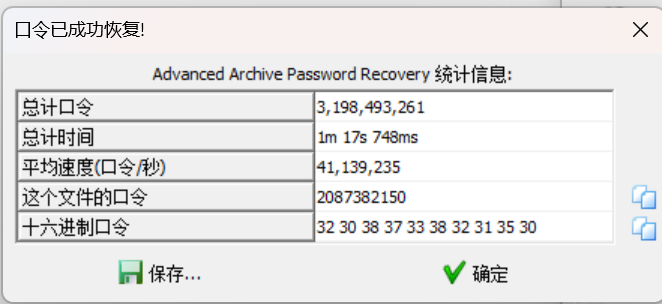
得到WHUCTF{Little_games_reall

2.数织

队友很强，直接手搓了。

得到y_train_your_brain_&_play

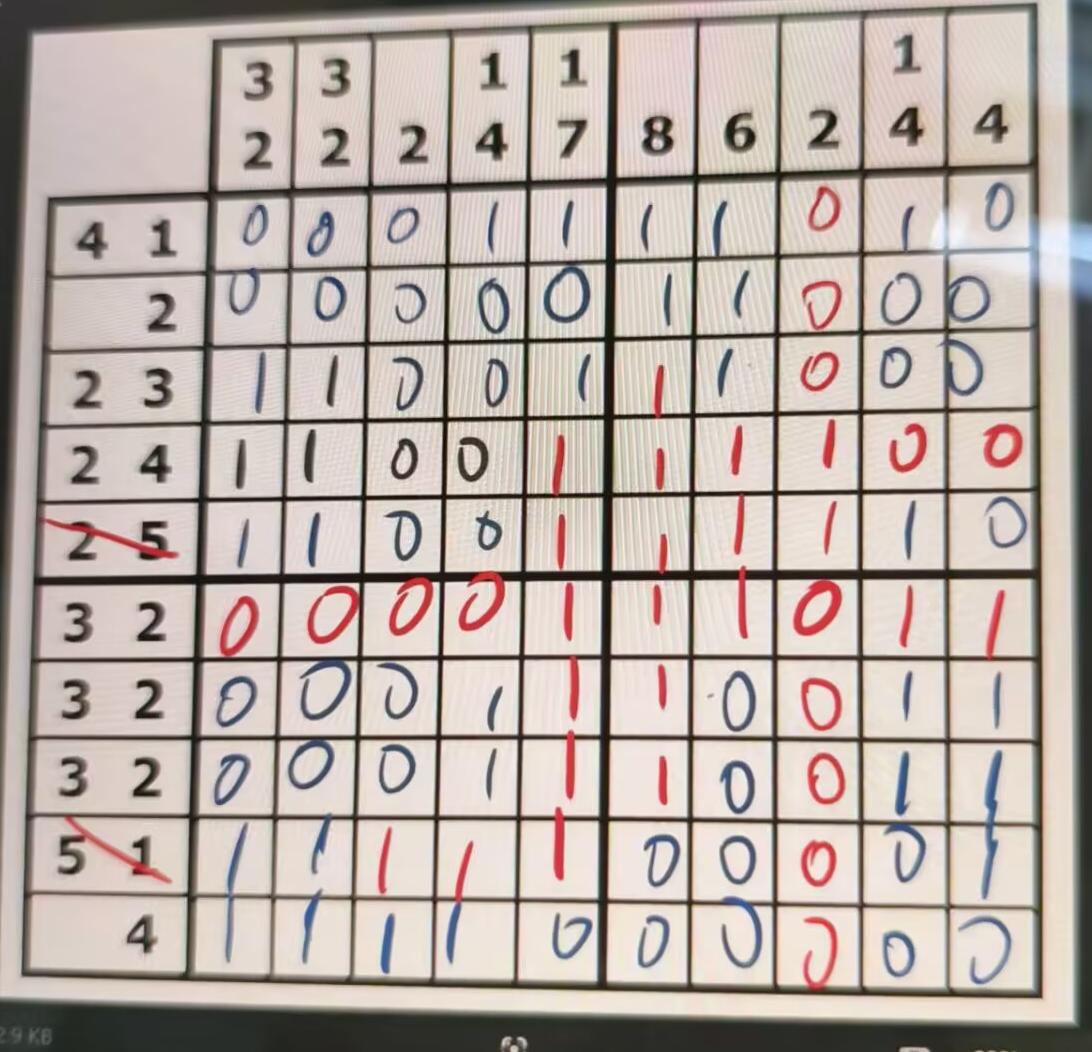
3.鬼脚图

直接白给了。。。

得到_more_in_cn.puzzle_website}

哪里有文档

附件是一个docx文档，而且直接给出了part1。

part2：ctrl+A一下，发现在文章最后，改一下字体颜色就看到了。
|525

part3：ctrl+F一下，搜索part，发现一个非常隐秘的文本框，放大一下，找到part3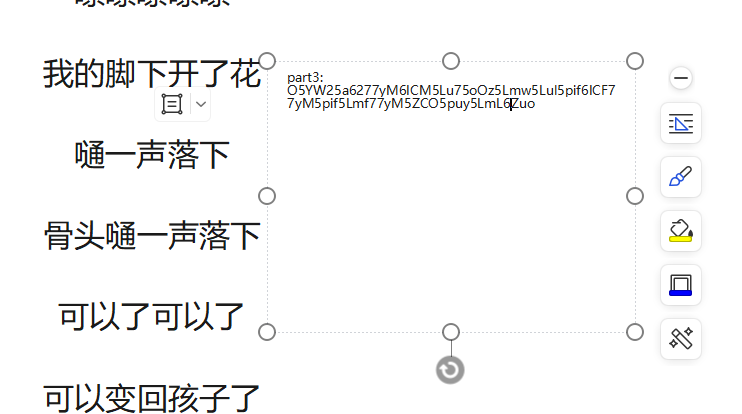
|525
part4： 由于docx文档本质是压缩包，可以解压出一个文件夹，在docprops文件夹下边的custom文件中发现part4.

part5： 在word文件夹下边的vbaProject.bin文件中发现非疑似part5的字符串，后来试了一下还真是。

解密器： 在文档页脚的地方发现有东西，换一下字体颜色便发现，by Abracadabra encoder，上网搜索之后发现是魔曰。

解密步骤： 将5段part拼接后进行base64解码，得到一段文字，

鹏无局，无以致天，光有能听，竹有善然，虽无楼鸢之彰，亦报以畅看瀚水，求将与其家，而任想买以星者，星也，后曲之雨，选之霞而称之茶也，寒冰悠见，写者旅之，叶流而清梦看也，报在莹鹤。

放在魔曰解码器中解码得到flag

WHUCTF{always_follow_your_heart}

行星防御理事会

附件为一个wav音频，放到Audacity中查看波形图，觉得类似sstv，放入RX-SSTV工具中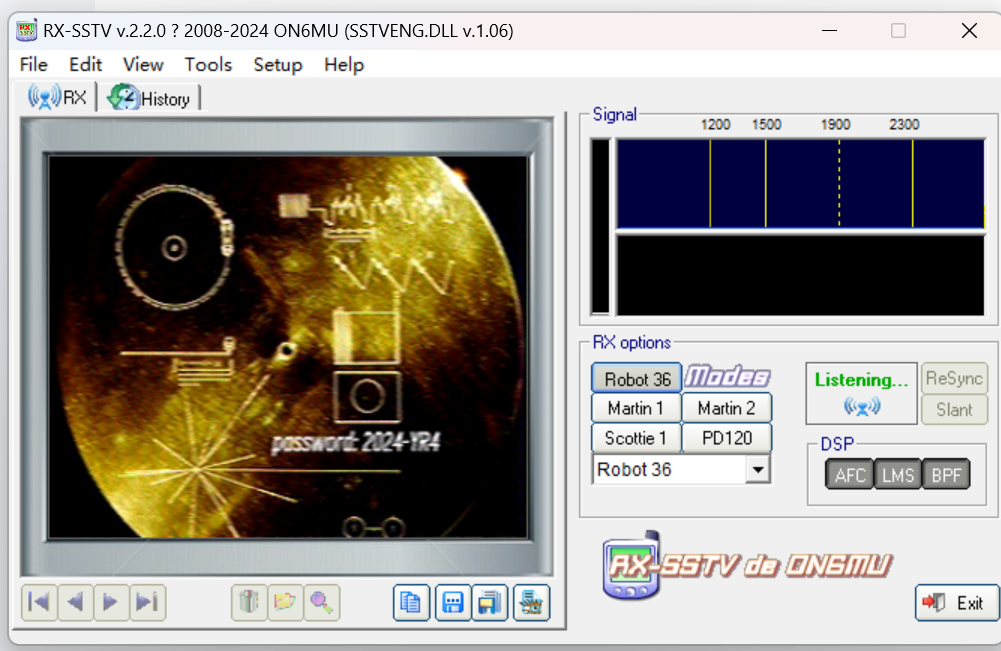
|625
发现有密码2024-YR4，联想需要密码的wav音频隐写，在Deepsound中输入密码后得到附件，解压后是一个变形过的二维码和一个变形脚本。编写恢复脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from PIL import Image
import numpy as np


def rotate(m: int, arr: np.ndarray):
    """将数组分割为 m x m 块，并将每块顺时针旋转 90 度"""
    h, w = arr.shape
    new_arr = np.zeros_like(arr)
    for i in range(0, h, m):
        for j in range(0, w, m):
            block = arr[i:i + m, j:j + m]
            rotated_block = np.rot90(block, k=-1)  # 顺时针旋转90度
            new_arr[i:i + m, j:j + m] = rotated_block

    return new_arr


if __name__ == "__main__":
    # 读取图片
    img = Image.open("QR_modified.png").convert("L")
    imgarr = (np.array(img) // 255).astype(np.uint8)
    imgarr = imgarr[::18, ::18]

    imgarr = rotate(5, imgarr)

    # 保存图片
    newimgarr = np.kron(imgarr, np.ones((18, 18)))
    newimg = Image.fromarray(newimgarr * 255).convert("L")
    newimg.save("QR.png")

    print("图片已保存为 QR.png")
#WHUCTF{much_ado_about_nothing}

|225
扫码得到flag。

青轴还是红轴

wireshark打开附件，发现全是USB协议流量，结合题目猜测是键盘流量。

在kali中使用tshark提取键盘流量

tshark -r raw_keyboard.pcapng -T fields -e usbhid.data > usbdata.txt

然后用脚本对提取出的流量进行处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
normalKeys = {"04": "a", "05": "b", "06": "c", "07": "d", "08": "e", "09": "f", "0a": "g", "0b": "h", "0c": "i",
            "0d": "j", "0e": "k", "0f": "l", "10": "m", "11": "n", "12": "o", "13": "p", "14": "q", "15": "r",
            "16": "s", "17": "t", "18": "u", "19": "v", "1a": "w", "1b": "x", "1c": "y", "1d": "z", "1e": "1",
            "1f": "2", "20": "3", "21": "4", "22": "5", "23": "6", "24": "7", "25": "8", "26": "9", "27": "0",
            "28": "<RET>", "29": "<ESC>", "2a": "<DEL>", "2b": "\t", "2c": "<SPACE>", "2d": "-", "2e": "=", "2f": "[",
            "30": "]", "31": "\\", "32": "<NON>", "33": ";", "34": "'", "35": "<GA>", "36": ",", "37": ".", "38": "/",
            "39": "<CAP>", "3a": "<F1>", "3b": "<F2>", "3c": "<F3>", "3d": "<F4>", "3e": "<F5>", "3f": "<F6>",
            "40": "<F7>", "41": "<F8>", "42": "<F9>", "43": "<F10>", "44": "<F11>", "45": "<F12>"}

shiftKeys = {"04": "A", "05": "B", "06": "C", "07": "D", "08": "E", "09": "F", "0a": "G", "0b": "H", "0c": "I",
            "0d": "J", "0e": "K", "0f": "L", "10": "M", "11": "N", "12": "O", "13": "P", "14": "Q", "15": "R",
            "16": "S", "17": "T", "18": "U", "19": "V", "1a": "W", "1b": "X", "1c": "Y", "1d": "Z", "1e": "!",
            "1f": "@", "20": "#", "21": "$", "22": "%", "23": "^", "24": "&", "25": "*", "26": "(", "27": ")",
            "28": "<RET>", "29": "<ESC>", "2a": "<DEL>", "2b": "\t", "2c": "<SPACE>", "2d": "_", "2e": "+", "2f": "{",
            "30": "}", "31": "|", "32": "<NON>", "33": "\"", "34": ":", "35": "<GA>", "36": "<", "37": ">", "38": "?",
            "39": "<CAP>", "3a": "<F1>", "3b": "<F2>", "3c": "<F3>", "3d": "<F4>", "3e": "<F5>", "3f": "<F6>",
            "40": "<F7>", "41": "<F8>", "42": "<F9>", "43": "<F10>", "44": "<F11>", "45": "<F12>"}
nums = []
keys = open('usbdata.txt')
for line in keys:
    if len(line) != 17:
        continue
    nums.append(line[0:2] + line[4:6])
keys.close()

output = ""
for n in nums:
    if n[2:4] == "00":
        continue
    if n[2:4] in normalKeys:
        if n[0:2] == "02":
            output += shiftKeys[n[2:4]]
        else:
            output += normalKeys[n[2:4]]

print('output :' + output.replace("<SPACE>"," "))

输出为output :ijniokj tfcfg fgtrdcv iuhbghj jkiuhnm ygvgh_ijnjkmn uhbn tgbnjujm ghytfvb_fghygvb ygbnju <DEL>_eszsd dfresxc hgvbhuhb_uyhbv dcfvg hbu hjkijnm uygbn eszsdx

低头看看键盘，就会发现每一组字母都是在键盘上拼出一个一个字母的形状。

最后得到prefer_blue_to_red_switch

Crypto

LFSR_Signin

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import *
flag = b"whuctf{}"

flag = list(bin(bytes_to_long(flag))[2:])
assert(len(flag) == 255)

for i in range(len(flag)):
    flag[i] = int(flag[i])

for i in range(2025):
    flag.append(flag[i] ^ flag[i+20] ^ flag[i+25] ^ flag[i+250] ^ flag[-1])
    print(flag[-1], end="")

#110000011011110000010101100011111101011011111111111111101011000111001010111000101111101100011011000110011000100010011111110111010110000111111111111101111011011101000000010011110010111000110100110011101110101010110001110100111001100011100001001000000011010011001101001000000000110110100101000110000011011100011100001000010001110000111110000110010001110001101011101110100011010000101101000000000001101111111001010100011110110001101010010100011010011010010110010110100011001100010010010110110010010001111010111100011101100001111111110101011010011111110101000110010000101011011101000000111000001011010010001010101101111111001100010001001011100100111000010100011001001111011110111111101100111001011100001110110110100010011010011111110010111001101000011000011111001101100111001111000010011110011111001010001111110001010100100011001000100011001010010111010000011101011001111111010010010101001010011010000010000100001010111000000000010011011110110001101010010101001010100100010110001001000101000001011111010110101110111100101001100101011000010000101010001010111010111010010110001111010000001101101100101111001010010010011010101110001101001111011010001000010111010011010001011011011000111101010001101110000100100011010011111110110000001101100010011000110100010101010010101100101011001001100010100111011101111100010111100010001101100101100111110101001111101000010110110011000111100110101001111001100110111100111111000101101101000011110011001101100111100111001001001001100101111101110111011111110110101000001100010110101101100100001110100110101100101011010101101101100011011000001111001010001110000110001001011001001110111110000001000011000011000101010101010010010100010011011000011100111011101111110100101111111001011010110010010011101011001011110001101110110110111110100000100001111100101000001101010000011001001100100010101111010100000010110010010111000000010010101001011001011001111001000100010100101000011110110101001011111011111001010111101111000001101101100101111010101100110000111011101100100000011001110011000110110100101010100

分析： 通过代码可以发现，生成时，每个最后边生成的二进制数字都是由前边的一些数字异或得到，逆向来分析，同理，每个靠前的数字也都可以由后边的一些数字得到。
由此，我们便可以从第255位开始，反向一个一个求出前255个数字。

解答：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Util.number import long_to_bytes
enc="110000011011110000010101100011111101011011111111111111101011000111001010111000101111101100011011000110011000100010011111110111010110000111111111111101111011011101000000010011110010111000110100110011101110101010110001110100111001100011100001001000000011010011001101001000000000110110100101000110000011011100011100001000010001110000111110000110010001110001101011101110100011010000101101000000000001101111111001010100011110110001101010010100011010011010010110010110100011001100010010010110110010010001111010111100011101100001111111110101011010011111110101000110010000101011011101000000111000001011010010001010101101111111001100010001001011100100111000010100011001001111011110111111101100111001011100001110110110100010011010011111110010111001101000011000011111001101100111001111000010011110011111001010001111110001010100100011001000100011001010010111010000011101011001111111010010010101001010011010000010000100001010111000000000010011011110110001101010010101001010100100010110001001000101000001011111010110101110111100101001100101011000010000101010001010111010111010010110001111010000001101101100101111001010010010011010101110001101001111011010001000010111010011010001011011011000111101010001101110000100100011010011111110110000001101100010011000110100010101010010101100101011001001100010100111011101111100010111100010001101100101100111110101001111101000010110110011000111100110101001111001100110111100111111000101101101000011110011001101100111100111001001001001100101111101110111011111110110101000001100010110101101100100001110100110101100101011010101101101100011011000001111001010001110000110001001011001001110111110000001000011000011000101010101010010010100010011011000011100111011101111110100101111111001011010110010010011101011001011110001101110110110111110100000100001111100101000001101010000011001001100100010101111010100000010110010010111000000010010101001011001011001111001000100010100101000011110110101001011111011111001010111101111000001101101100101111010101100110000111011101100100000011001110011000110110100101010100"
c=[0 for _ in range(2280)]
for i in range(2025):
    c[i+255] = int(enc[i])
for i in range(254,-1,-1):
    a=c[i+255]^c[i+254]^c[i+250]^c[i+20]^c[i+25]
    """ if a == c[i]:
        print(1) """
    c[i]=a
res=''
for i in range(255):
    res+=str(c[i])
print(res)
m=long_to_bytes(int(res,2))
print(m)
#print(c)

得到flagwhuctf{quit3_ea5y_Sign1n_R1ght?}

RSAASR

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from Crypto.Util.number import getPrime, isPrime, bytes_to_long, long_to_bytes


def generate(bit):
    while True:
        p = getPrime(bit)
        q = rev(p)
        if isPrime(q):
            break
    return p, q


rev = lambda x: int(bin(x)[:1:-1], 2)   # 二进制反转整数
flag = b"??????"
p, q = generate(512)                    #p,q相互反转
n = p * q
e = 65537
c = pow(bytes_to_long(flag), e, n)
print(f"n={n}")
print(f"e={e}")
print(f"c={c}")
"""
n=89260288112458610375700543707493254232809306221431627423709616690294586688526862549905410606087786699242563057156677052913617284849136716660502920085006747882186134482309361626185003661858419446057779826705477210404882478906671799290032009310469036065257789664458482249297907582602310789531951177426393110643
e=65537
c=34953739673730018843655174314108340461262205663805875643136393046216892771730195951086950749299233260612871271352091804579992550715616098448464010205976283620661044089962336249776561849400241337436006809354102892524119722533361144592982143227173415365371111087024439252557012289555411199194971295453523635612
"""

分析： 剪枝题，直接打板子，具体可参考Crypto趣题-剪枝 | 糖醋小鸡块的blog
解答：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from Crypto.Util.number import *

n = 89260288112458610375700543707493254232809306221431627423709616690294586688526862549905410606087786699242563057156677052913617284849136716660502920085006747882186134482309361626185003661858419446057779826705477210404882478906671799290032009310469036065257789664458482249297907582602310789531951177426393110643
c = 34953739673730018843655174314108340461262205663805875643136393046216892771730195951086950749299233260612871271352091804579992550715616098448464010205976283620661044089962336249776561849400241337436006809354102892524119722533361144592982143227173415365371111087024439252557012289555411199194971295453523635612
e = 65537

def find(ph,qh,pl,ql):
    l = len(ph)
    tmp0 = ph + (512-2*l)*"0" + pl
    tmp1 = ph + (512-2*l)*"1" + pl
    tmq0 = qh + (512-2*l)*"0" + ql
    tmq1 = qh + (512-2*l)*"1" + ql
    if(int(tmp0,2)*int(tmq0,2) > n):
        return 
    if(int(tmp1,2)*int(tmq1,2) < n):
        return
    if(int(pl,2)*int(ql,2) % (2**(l-1)) != n % (2**(l-1))):
        return

    if(l == 256):
        pp0 = int(tmp0,2)
        if(n % pp0 == 0):
            pf = pp0
            qf = n//pp0
            phi = (pf-1)*(qf-1)
            d = inverse(e,phi)
            m1 = pow(c,d,n)
            print(long_to_bytes(m1))
            exit()

    else:
        find(ph+"1",qh+"1","1"+pl,"1"+ql)
        find(ph+"0",qh+"1","1"+pl,"0"+ql)
        find(ph+"1",qh+"0","0"+pl,"1"+ql)
        find(ph+"0",qh+"0","0"+pl,"0"+ql)

find("1","1","1","1")

Pollard & Williams

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
from Crypto.Util.number import *
import os

flag = b'whuctf{}'
blen = 256


def rsa(p, q, message):
    n = p * q
    e = 65537

    pad_length = n.bit_length() // 8 - len(message) - 2
    message += os.urandom(pad_length)
    m = bytes_to_long(message)
    return n, pow(m, e, n)


def part1(message1, message2):
    while True:
        p1 = getPrime(blen)         #256bit
        p2 = (p1 - 1) // 2
        if isPrime(p2):
            break

    q1 = getPrime(blen)
    q2 = getPrime(blen)

    return rsa(p1, q1, message1), rsa(p2, q2, message2)


def part2(message1, message2):
    while True:
        p1 = getPrime(blen)
        p2 = (p1 + 1) // 2
        if isPrime(p2):
            break

    q1 = getPrime(blen)
    q2 = getPrime(blen)

    return rsa(p1, q1, message1), rsa(p2, q2, message2)


assert len(flag) == 44              #长度为44
l = len(flag) // 4                  #11
m1, m2, m3, m4 = [flag[i * l: i * l + l] for i in range(4)] #分成四份
c1, c2 = part1(m1, m2)
c3, c4 = part2(m3, m4)

print(f'{c1 = }')
print(f'{c2 = }')
print(f'{c3 = }')
print(f'{c4 = }')

# c1 = (6053032598894343876848386724367478876865502990878797490385487692233771017587839889683279773931697102081210221515871925626229356354906807395177342943323369, 4066195854081844630643812355140109730178549671457699640787009592379117222130777528564788537029636082768525403919530491221982157867347461546035515101540809)
# c2 = (3881600892538209342174115382004433032693183438455968854185245139152150453077746028435728337685187304179257593974737056409431270271087770400534952463611803, 3170419555737452151768856928448822332346045957475336562622244748908867061340721719260259808765271614258250388620180512676045609008728482012225062330421389)
# c3 = (12299016617136978588548772285625358530978334196485520160172325214608426825374255755330322407319092229940503630270734074076341447314630647646764214262929507, 318163940794629731124968470499655451861010987042419720693423620230895540439020747998494269609254222775880714679954773027280497632868550785421041286883861)
# c4 = (4549315768074822845197072475333248869579555413221208949230121240611191001190288208256119819724334902434536556333152862828649067092565476816480268615884657, 1882968780168858989700488482275734089425710600149658668167954773629584030303631176914870357507995175067079535271674721507969999430710585448040194277936142)

分析： 可以看出，flag被分成了四部分，而且前两个之间存在关系，后两个之间存在关系。

重点在于p2 = (p1 - 1) // 2,p2 = (p1 + 1) // 2，我们来逐个分析。

Part1：

$$ \because p_2=(p_1-1)//2 \\ \therefore 2*N_2=2*p_2*q_2=(p_1-1)q_2 \\ 即 p_1-1|2*N2 \\ \therefore a^{2*N_2} \equiv a^{q_2*(p1-1)}\equiv1 \mod p_1 \\ \therefore a^{2*N_2}-1 = kp_1 \\ 当然 a^{2*N_2}-1 \mod N_1 = kp_1 \\ \therefore p_1=gcd(a^{2*N2}-1 \mod N_1,N_1) $$

之后$q_1,p_2,q_2$便都能求出来，之后就是简单的RSA

Part2:

对于william p+1光滑算法中，p+1为光滑数，设B为p+1最大的光滑因子，要求得下标为B的阶乘B!卢卡斯序列，目的就是保证(p+1)|B!，而本题中能够看出$2*N_4=(p_3+1)*q_4$必然是$(p_3+1)$的整数倍。

之后就利用卢卡斯序列的性质来求$p_3。即p_3|(V_{2*N_4}-2)$

$\therefore p_3|gcd(V_{2*N_4}-2,N_3)$

$\therefore p_3=gcd(V_{2*N_4}-2\mod N_3,N_3)$

之后同上，脚本如下

解答：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
from sympy import Matrix
from Crypto.Util.number import long_to_bytes
import gmpy2

c1 = (6053032598894343876848386724367478876865502990878797490385487692233771017587839889683279773931697102081210221515871925626229356354906807395177342943323369, 4066195854081844630643812355140109730178549671457699640787009592379117222130777528564788537029636082768525403919530491221982157867347461546035515101540809)
c2 = (3881600892538209342174115382004433032693183438455968854185245139152150453077746028435728337685187304179257593974737056409431270271087770400534952463611803, 3170419555737452151768856928448822332346045957475336562622244748908867061340721719260259808765271614258250388620180512676045609008728482012225062330421389)
c3 = (12299016617136978588548772285625358530978334196485520160172325214608426825374255755330322407319092229940503630270734074076341447314630647646764214262929507, 318163940794629731124968470499655451861010987042419720693423620230895540439020747998494269609254222775880714679954773027280497632868550785421041286883861)
c4 = (4549315768074822845197072475333248869579555413221208949230121240611191001190288208256119819724334902434536556333152862828649067092565476816480268615884657, 1882968780168858989700488482275734089425710600149658668167954773629584030303631176914870357507995175067079535271674721507969999430710585448040194277936142)
e=65537
n1,n2,n3,n4=c1[0],c2[0],c3[0],c4[0]
enc1,enc2,enc3,enc4=c1[1],c2[1],c3[1],c4[1]
#前半
p1=gmpy2.gcd(pow(2,2*n2,n1)-1,n1)
q1=n1//p1
p2=(p1-1)//2
q2=n2//p2
phi1=(p1-1)*(q1-1)
phi2=(p2-1)*(q2-1)
d1=gmpy2.invert(e,phi1)
d2=gmpy2.invert(e,phi2)
m1=pow(enc1,d1,n1)
m2=pow(enc2,d2,n2)
#print(m1,m2)
ans1=long_to_bytes(m1)[:11]
ans2=long_to_bytes(m2)[:11]
print(ans1,ans2)

#后半
#矩阵快速幂
def matrix_pow_mod(matrix, exp, mod):
    result = Matrix.eye(matrix.rows)  # 单位矩阵
    base = matrix
    while exp > 0:
        if exp % 2 == 1:
            result = (result * base) % mod
        base = (base * base) % mod
        exp //= 2
    return result

#计算卢卡斯序列
def lucas_nth_mod(n, P, m):
    M = Matrix([[P, -1], [1, 0]])      # 转换为矩阵形式
    vec = Matrix([P, 2])               # 初始向量 L1 = P, L0 = 2
    M_n = matrix_pow_mod(M, n, m)
    result = M_n * vec
    return result[1] % m

P = 3                                   #要求为大于2的整数
n = n4*2
v_n = lucas_nth_mod(n, P, n3)        #下标为n的卢卡斯序列

p3=gmpy2.gcd(int(v_n)-2,n3)
q3=n3//p3
p4=(p3+1)//2
q4=n4//p4
phi3=(p3-1)*(q3-1)
phi4=(p4-1)*(q4-1)
d3=gmpy2.invert(e,phi3)
d4=gmpy2.invert(e,phi4)
m3=pow(enc3,d3,n3)
m4=pow(enc4,d4,n4)
#print(m3,m4)
ans3=long_to_bytes(m3)[:11]
ans4=long_to_bytes(m4)[:11]
print(ans3,ans4)

print(ans1+ans2+ans3+ans4)
#b'whuctf{real' b'ly_sp3cia1_'
#b'P0llard_4nd' b'_w1ll1ams!}'
#b'whuctf{really_sp3cia1_P0llard_4nd_w1ll1ams!}'

ez_lattice

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from Crypto.Util.number import *
flag = b"whuctf{}"
blen = 512

l = len(flag) // 4                          
n = 2
X = []
a = [bytes_to_long(flag[i * l: i * l + l]) for i in range(2)]   #前两个四分之一段分别转换成整数
b = 0
p = getPrime(blen)                              #512bit素数

for i in range(2):
    X.append(getRandomNBitInteger(blen))        #512bit整数
    b = (a[i] * X[i]) % p
    assert b.bit_length() < 110

print("p =", p)
print("X =", X)

# p = 12478746590758967738992827236548867094406642228843048782158822830242432957850861746109083849369751421558416546441433265483311369062332823391326650330844473
# X = [4370703796271085517745653374714633557060694569231794372714420305839580193452505356598920188429238758568075323630107438853033389535935767953293146851021439, 5636765597544539887670148818611437395262628189014720546978418282055551396918915796702935478309173130501906553399905160951176701403838275497327658585404887]

n = 2
X = []
a = [bytes_to_long(flag[i * l: i * l + l]) for i in range(2, 4)]
print(a)
p = getPrime(blen)

for i in range(n):
    X.append(getRandomNBitInteger(blen))
    b = (a[i] * X[i]) % p
    assert b.bit_length() <= 55

s = getRandomNBitInteger(55)
P = p - s

print("P =", P)
print("X =", X)

# P = 8064317391291915578249751043887298750752952396481901402238164933671762816998644264248732894561122039999833298392825353792148892469165631966482732750535761
# X = [6042201174605160506707043360458329015685676206288676104013330039569480295420873678739841513174948925787517746114885517054730046775608073287427260847787072, 6232867934334525782602291010514616748943593081406115516232887372014738839717093295759414233886061184914495957664550361507367497641317336980894814940037711]

参考： Wiener’s v.s Lattices —— Ax≡y(mod P)的方程解法笔记 | Tover’s Blog

分析： flag又被分成了两部分，感谢出题人总是先送我一半flag。

part1: 非常常规的格，构造

$$ (a[0],a[1],k) \begin{pmatrix} 1 & 0 & X[0] \\ 0 & 1 & X[1] \\ 0 & 0 & p \\ \end{pmatrix} =(a[0],a[1],b_1+b_2) $$

part2:

参考了大佬博客之后才有思路，总之就是要把X[2],X[3]分开来讨论，构造格

AM=B :

$$ (k_1k_2,a_1k_2,a_2k_1,a_1a_2) \\ \begin{pmatrix} 1 & P & 0 & P^2 \\ 0 & X_1 & X_1 & X_1P \\ 0 & 0 & -X_2 & X_2P \\ 0 & 0 & 0 & X_1X_2\\ \end{pmatrix}\\ =(k_1k_2,k_2(b_1-sk_1),b_1k_2-b_2k_1,(b_1-k_1s)(b_2-k_2s) $$

由于这个格并不满足Hermite定理，因此需要配平，配平系数可以参考大佬博客。

$$ B \approx (P^{2\alpha},P^{2\alpha+\gamma},P^{\alpha+\beta},P^{2\alpha+2\gamma})\\ \begin{pmatrix} P^{2\gamma} & 0 & 0 & 0\\ 0 & P^{\gamma} & 0 & 0 \\ 0 & 0 & P^{\alpha-\beta+2\gamma} & 0 \\ 0 & 0 & 0 & 1\\ \end{pmatrix} $$

其中$\gamma=\frac12,\alpha=\frac{5}{14},\beta=0$

求出矩阵B之后再乘上M的逆，从而得到矩阵A，再利用a中关系求出$a_1,a_2$

解答：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from Crypto.Util.number import long_to_bytes
import gmpy2

#part1
p = 12478746590758967738992827236548867094406642228843048782158822830242432957850861746109083849369751421558416546441433265483311369062332823391326650330844473
X = [4370703796271085517745653374714633557060694569231794372714420305839580193452505356598920188429238758568075323630107438853033389535935767953293146851021439, 5636765597544539887670148818611437395262628189014720546978418282055551396918915796702935478309173130501906553399905160951176701403838275497327658585404887]

M = matrix(ZZ,[[1,0,X[0]],[0,1,X[1]],[0,0,p]])
L = M.LLL()[0]
a1=long_to_bytes(abs(L[0]))
a2=long_to_bytes(abs(L[1]))
print(a1,a2)
#b'whuctf{' b'Lattice'

#part2
P = 8064317391291915578249751043887298750752952396481901402238164933671762816998644264248732894561122039999833298392825353792148892469165631966482732750535761
X = [6042201174605160506707043360458329015685676206288676104013330039569480295420873678739841513174948925787517746114885517054730046775608073287427260847787072, 6232867934334525782602291010514616748943593081406115516232887372014738839717093295759414233886061184914495957664550361507367497641317336980894814940037711]

x1,x2 = X
a=5/14
M1=int(P^0.5)
M2=int(P^(1+a))

L2=Matrix(ZZ,[[P,   M1*P,       0,    P^2],
            [0,    M1*x1,   M2*x1,   x1*P],
            [0,        0,  -M2*x2,   x2*P],
            [0,        0,       0,  x1*x2]])
B=L2.LLL()[0]
A=B*L2^(-1)

#print(A)
a3=gcd(A[1],A[3])        #因为没有保证a3,a4为素数，其实是k*a3，这里k刚好是1，否则可能需要爆破
a4=A[3]//a3
#print(a3)
#print(a4)
#print(a3*a4)

a3=long_to_bytes(int(a3))
a4=long_to_bytes(int(a4))
print(a3,a4)
print(a1+a2+a3+a4)
#b'_1s_P0w' b'erFu1!}'
#b'whuctf{Lattice_1s_P0werFu1!}

Siesta’s_revenge

题目：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from Crypto.Util.Padding import pad
from Crypto.Util.number import *
from Crypto.Cipher import AES

from hashlib import *
flag = b"whuctf{}"
blen = 512

p = getPrime(blen)
s = getRandomNBitInteger(100)
P = p + s

t = 2
X = []
a = [getPrime(160) for _ in range(t)]
for i in range(t):
    X.append(inverse(a[i], p))

key = sha256(str(a[0]*a[1]).encode()).digest()[:16]
iv = b"0" * 16
AES = AES.new(key, AES.MODE_CBC, iv)

print("X =", X)
print("P =", P)
print("ct =", AES.encrypt(pad(flag, AES.block_size)))

# X = [1266403423628708294851978766647131186574350037928491893316575383770634141679199238688724846443316942748685589080912612989737322832820423142859211423222170, 10633805933378187507165706136587361125130747673943368523389315948924728188453225153073019422908293191827053741582511390426559341625596650317484672418362991]
# P = 12727949469666331910572325155797935927989546075198211256583307434798528241134917675474139742863165705376701853130873014549089300596914514323642506815012401
# ct = b'\xe9\x87\x942\xbc\x94`t\x85^r\xb8\xd2\x00\xfb\xb0Ni\x08\xcf\x07\xf1\xae\x95U{\xf1\xd4\xda}@H'

分析： 怎么说呢，跟上题不能说十分类似吧，只能说一模一样，只是s变大了而已，但实践证明，它并没有影响我们格攻击成功。（所以说不理解出题人的预期效果是什么，希望能讲一讲）

那么攻击思路就同上

解答：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from Crypto.Util.Padding import pad
from Crypto.Util.number import *
from Crypto.Cipher import AES

from hashlib import *

X = [1266403423628708294851978766647131186574350037928491893316575383770634141679199238688724846443316942748685589080912612989737322832820423142859211423222170, 10633805933378187507165706136587361125130747673943368523389315948924728188453225153073019422908293191827053741582511390426559341625596650317484672418362991]
P = 12727949469666331910572325155797935927989546075198211256583307434798528241134917675474139742863165705376701853130873014549089300596914514323642506815012401
ct = b'\xe9\x87\x942\xbc\x94`t\x85^r\xb8\xd2\x00\xfb\xb0Ni\x08\xcf\x07\xf1\xae\x95U{\xf1\xd4\xda}@H'

x1,x2 = X
a=5/14
M1=int(P^0.5)
M2=int(P^(1+a))

L2=Matrix(ZZ,[[P,   M1*P,       0,    P^2],
            [0,    M1*x1,   M2*x1,   x1*P],
            [0,        0,  -M2*x2,   x2*P],
            [0,        0,       0,  x1*x2]])

B=L2.LLL()[0]
A=B*L2^(-1)

#print(A)
a=gcd(A[1],A[3])
b=gcd(A[2],A[3])
ans1=long_to_bytes(int(a))
ans2=long_to_bytes(int(b))
#print(ans1,ans2)

key = sha256(str(a*b).encode()).digest()[:16]
iv = b"0" * 16
AES = AES.new(key, AES.MODE_CBC, iv)
print("mt =", AES.decrypt(ct))
#mt = b'whuctf{You_w1ll_never_kn0w_1t!}\x01'

总结

打ctf以来最有感觉的一场比赛，酣畅淋漓，也是燃尽了，感谢队友的带飞。

总结自己的做题量还是太少，对于很多原本应该一眼看出来的问题还是犹犹豫豫的，甚至不敢相信自己思路是对的，后来被hint拉回原本的思路才坚持做出正确结果。

因此日后还要加倍努力，争取不拖队友后腿！

WriteUp
#CTF
WHUCTF2025 WP
http://ramoor.github.io/2025/03/31/WHUCTF 2025-WP/
作者
Ramoor
发布于
2025年3月31日
许可协议