Introduction To Modern Cryptography学习随笔

在老师的推荐下，我学习了《Introduction To Modern Cryptography》一书的部分内容，本文用来记录阅读过程中的一些随笔，可能会有些潦草，如果往后有了更深的认识，会回来继续完善。

这是我第一次大篇幅阅读英文书籍，刚开始读确实比较难以接受，因为要频繁地搜索一些单词含义，有时候一些地方中文翻译之后与原文含义相差甚远，因此还是硬着头皮大概过了一下原文。
读的过程中我发现本书会花费大量的篇幅去论述一个定义，很适合初学者去接触理解每个定义的深层次含义。

3.私钥密码

3.1 计算安全性

计算安全相对于信息论安全（完美安全）包含两个放松

• 仅针对有效攻击者（合理时间或有限资源）
• 允许攻击者有较小概率成功（概率足够小，可忽略不计）

3.1.1 具体方法

计算安全的具体方法通过明确限定时间和计算资源下，攻击者的最大成功概率，来量化加密方案的安全性。具体的安全性定义形式如下：

• 如果任意一个时间上限为$t$的攻击者都不能以成功概率高于$\epsilon$的概率破解加密方案，这个方案便是$(t,\epsilon)-安全$ 的。

3.1.2 渐近方法

具体安全性方法存在一些技术和理论上的困难。因此在抽象描述方案时使用，使用渐近方法。引入安全性参数$n$，并让其与密钥长度对应，把对手的运行时间和成功概率视为安全参数的函数。

渐近法详细说明

• 有效算法： 将“有效对手”等同于运行时间在$n$的多项式内的随机化（即概率性）算法。这意味着存在某个多项式$p$，当安全参数为$n$时，对手的运行时间不超过$p(n)$。
• 可忽略成功率： 将“成功概率小”这一概念等同于小于$n$的任何逆多项式的成功概率。即$\epsilon < \frac{1}{p(n)}$

多项式时间： 时间复杂度为$O(1)、O(nlog_n)、O(n^k)，其中k为某个常数$，等形式所需要的时间的为多项式时间。
非（超）多项式时间： 如时间复杂为$O(n!)、O(a^n)$，等算法所需要的时间为非（超）多项式时间。

总结

任何安全定义由两部分组成：

• 对方案的“攻破”（即安全目标）
• 对对手能力的详细说明（即威胁模型）

渐近安全定义：
如果每个ppt攻击者A执行某个特定类型的攻击，对于每个多项式$p(·)$，存在一个整数$N$，当安全参数$n$大于$N$时，攻击者成功破解的概率小于$\frac {1}{p(n)}$​，成功概率小于$\frac {1}{p(n)}$，则这个方案是安全的。

ppt攻击者：即“概率多项式时间（probabilistic polynomial-time）攻击者”。这意味着攻击者是一个随机化算法，其运行时间是安全参数n的多项式函数。

论渐近安全的定义选择

两个选择：

• 将有效的对抗策略与概率多项式时间算法相对应，
• 将小的成功概率等同于可忽略的概率

宽松的必要性

完美安全的限制： 密钥空间|K|必须和密文空间|M|一样大，不现实。

3.2 定义计算安全加密

针对私钥加密的计算安全性定义

3.2.1 基本安全定义（EAV安全）

EAV安全：即Eavesdropper Attack Security，攻击者仅观察单个密文，核心在于不可区分性。

针对仅密文攻击的安全性，即对手只观察到密文，或者给定密钥只能加密单个消息。

• 定义动机
  威胁模型：定义攻击者的假设能力，只能观察到单个密文,并在多项式时间内运行。
  安全目标：定义什么情况下加密方案被认为是被“破解”的，安全目标是攻击者无法从密文中获取任何关于明文的部分信息

这里的安全目标只是一个思想，这个思想概念的明确化在后边的语义安全定义给出，但由于语义安全较为复杂且难以处理，这里介绍一个与语义安全等价的定义——不可区分性。

• 窃听者存在下的不可区分性
  定义：一个私钥加密方案$Π$是“在窃听者存在的情况下不可区分的”，如果对于所有概率多项式时间攻击者A，存在一个可忽略函数$negl$，使得对于所有安全参数n：
  $Pr[PrivKeav_{A,Π}​(n)=1]≤\frac 12​+negl(n)$
  等效表述：
  $∣Pr[out_A​(PrivKeav_{A,Π}​(n,0))=1]−Pr[out_A​(PrivKeav_{A,Π}​(n,1))=1]∣≤negl(n)$

揭示明文长度

默认的安全加密定义中，不要求加密方案隐藏明文长度，但几乎所有常用的加密方案都会泄露明文长度（或其近似值）
明文长度泄露可能导致的问题：

• 简单数字/文本数据： 对于敏感信息可能会造成泄露，如个人收入位数不同也就可能暴露收入水平
• 自动补全功能： 这个自动补全列表大小可能揭示用户迄今为止输入的字母
• 数据库搜索： 返回的记录数量可能会泄露用户搜索的内容
• 压缩数据： 较短的压缩明文可能表明原始明文存在大量冗余

3.2.2 语义安全

语义安全性：语义安全性是第一个被提出的计算安全加密定义，它正式概念化了“攻击者无法从密文中获取任何关于明文的部分信息”这一概念。

通常，一个加密算法被认为是语义安全的，当且仅当它满足选择明文攻击（chosen-plaintext attack，CPA）的安全性。

区分一下不同难度的攻击，从上到下难度递减：

• 唯密文攻击（COA）：
  • 条件：已知一个或多个密文
  • 目标：确定明文
• 已知明文攻击（KPA）：
  • 条件：已知一个或多个相同密钥加密的明-密文对
  • 目标：确定其他密文对应的明文
• 选择明文攻击（CPA）：
  • 条件：可以选择明文进行加密，并得到加密结果
  • 目标：确定明文
• 选择密文攻击（CCA）：
  • 条件：可以选择密文进行解密，并得到解密结果（通常不能对所要求的密文进行解密）
  • 目标：确定所要求的密文对应的明文

下面再引出CPA安全和CCA安全的理解：

• CPA安全： 针对加密方案而言，已知两个明文，对其中一个加密得到密文，攻击者无法很好地判断这个密文对应哪个明文。
• CCA安全： 针对加密方案而言，已知两个密文，对其中一个解密得到明文，攻击者无法很好地判断这个明文对应哪个密文。

• 语义安全
  定义：一个私钥加密方案是语义安全的，如果对于任何ppt算法A，存在一个ppt算法$A_0$，使得对于任何ppt算法Samp和多项式时间可计算函数f和h，以下概率是可忽略的：
  $Pr[A(1^n,Enck(m),h(m))=f(m)]−Pr[A_0​(1^n,∣m∣,h(m))=f(m)]$

语义安全的等价性：
一个私钥加密方案在窃听者存在的情况下具有不可区分的加密当且仅当它是语义安全的。

语义安全与监听者存在下的不可区分性等价，但比不可区分性更为复杂和难以处理。

3.3 构建EAV安全加密方案

在构建EAV安全加密方案之前，先引入伪随机生成器，因为它通常用来生成加密密钥。

3.3.1 伪随机生成器（PRG）

定义：
伪随机生成器是一个高效、确定性的算法，将一个较短的均匀随机字符串（seed）转换为更长的“看起来均匀”的字符串（伪随机字符串）

一个好的PRG应满足的条件：

• 均匀性：输出的比特串应该足够均匀地分布在所有可能地比特串中
• 可预测性：在有seed的情况下可预测
• 不可区分性：在多项式时间内不能区分PRG输出和真正随机的输出

伪随机生成器G的输出并不是真正的均匀字符串

种子及长度：
seed就类似加密方案中的密钥，必须均匀且必须足够长防止暴力攻击，还需要进行保密
关于伪随机数的存在：
虽然我们无法无条件地证明伪随机生成器的存在，但有理由相信它们存在。例如，如果单向函数存在，则可以构造伪随机生成器。
实际构造：有许多实际的伪随机生成器（如流密码）被广泛使用，目前尚未发现有效的区分器。

3.3.2 规约证明

通常情况下，证明某个密码构造$Π$是安全的，只需要某个基础问题$X$是困难的，我们需要通过提供一个显式的规约来证明，该规约说明如何将任何成功“破解”$Π$的有效攻击者$A$转化为一个有效算法$A’$，该算法$A’$可以解决$X$。

个人理解：就是将一个方案的安全性建立在某个困难问题上。

3.3.3 伪随机数生成器的EAV安全

加密方案

• 构造：使用PRG G，其扩展因子为$l(n)$，构造一个固定长度的私钥加密方案。
• 关键生成：$Gen(1^n)$输出一个均匀随机的n位种子k。
• 加密：$Enc(k, m)$使用PRG G将种子k扩展为$l(n)$位的伪随机字符串，然后与明文m进行XOR得到密文c。
• 解密：$Dec(k, c)$使用PRG G将种子k扩展为$l(n)$位的伪随机字符串，然后与密文c进行XOR得到明文m。

规约-讨论

目标：证明如果G是一个PRG，那么上述构造的加密方案是EAV-secure的。
证明思路：通过归约证明，将攻击者A的成功概率与PRG G的伪随机性联系起来。

• 步骤1：固定一个攻击者A，其成功概率为$ε(n)$。
• 步骤2：构造一个区分器D，它使用A来区分PRG G的输出和均匀随机字符串。
• 步骤3：分析D的行为，证明如果G是PRG，那么D无法以非可忽略的概率区分G的输出和均匀随机字符串。
• 步骤4：得出结论，A无法以非可忽略的概率成功攻击加密方案。

具体安全性

如果G是$(t, ε)-PRG$，那么加密方案是$(t - t_0, ε)-secure$，其中$t_0$是一个小的常数。
如果攻击者A在时间$t - t_0$内运行，那么D在时间$t$内运行。由于G是$(t, ε)-PRG$，D无法以超过$ε$的概率区分G的输出和均匀随机字符串，因此A无法以超过$ε$的概率成功攻击加密方案。

3.4 更强的安全概念

3.4.1 多次加密的安全性

前面EAV安全只考虑了单个密文的安全性。
多次加密安全定义：
实验定义：引入了一个新的实验$PrivK^{mult}_{A,Π}(n)$，用于评估加密方案在多消息场景下的安全性。

1. 攻击者输出消息列表：攻击者A输出两组等长的消息列表$\vec M_0$和$\vec M_1$，每组包含t个消息，且每对消息$(m_0,i, m_1,i)$长度相同。
2. 密钥生成和加密：生成一个密钥k，随机选择一个比特b，对每组消息列表中的消息进行加密，得到密文列表$\vec C$。
3. 攻击者猜测：攻击者A观察密文列表$\vec C$，并输出一个比特$b’$。
4. 实验结果：如果$b’ = b$，则实验输出1，表示攻击者成功；否则输出0。

概率加密的必要性

为了实现多次加密的安全性，加密方案必须引入随机性，使得即使加密相同的消息，也会产生不同的密文。

流密码安全多次加密方案

同步模式： 密钥流足够长，双方同步通讯，得知已使用过的密钥流的位数，去掉已使用过的位数，往后截取新的密钥进行使用
非同步模式： 设置一个初始向量$IV$，生成密钥流时添入不同$IV$，保证每次生成的结果不一样。

3.4.2 选择明文攻击和CPA安全性

定义：选择明文攻击是指攻击者能够选择某些明文，并观察这些明文被加密后的密文。这种攻击模拟了攻击者对加密过程的部分控制能力。

CPA安全性

现代加密的最低要求：CPA安全性是现代加密方案应满足的最低安全要求。它确保即使攻击者能够选择某些明文并观察其密文，也无法获取关于其他未知消息的任何信息。
更强的安全性：虽然CPA安全性是最低要求，但实际应用中通常需要更强的安全性。

3.4.3 CPA安全性和多消息加密

等价性：如果一个加密方案能够抵抗单次加密的选择明文攻击，那么它也能够抵抗多消息加密的选择明文攻击

• 固定长度vs任意长度消息
  构造方法： 将任意长度的消息拆分为各个固定长度的消息分别加密

3.5 构建一个CPA安全的加密方案

3.5.1 伪随机函数（PRFs）和置换

PRFs：伪随机函数是一种“看起来随机”的函数。与伪随机生成器类似，伪随机函数的安全性是通过其输出与真正随机函数的输出难以区分来定义的

• 伪随机函数和伪随机发生器
  从PRF构造PRG：可以通过在一系列不同输入上评估PRF来构造PRG。例如，定义$G(s) = F_s(1) || F_s(2) || … || F_s(l)$，其中$l$是所需的输出长度。
  从PRG构造PRF：可以将PRG的输出解释为一个查找表，从而构造一个PRF。但这种方法仅适用于小输入长度。

PRG要求输出长度必须大于输入长度，但PRF允许输出长度与输入无关

伪随机置换

定义： 伪随机置换是一种特殊的PRF，其中输入和输出长度相同，并且对于每个密钥k，$F_k$是一个双射（即置换）。

• 强伪随机置换
  定义： 强伪随机置换不仅要求$F_k$与均匀随机置换不可区分，还要求即使区分器D同时访问$F_k$和其逆函数$F_k^{-1}$，也无法区分。

3.5.2 基于伪随机函数的CPA安全

需要引入一个随机变量$r(如上边流密码非同步模式中的IV)$

4.消息认证码（MAC）

保证真实性和完整性

4.1 消息完整性

4.1.1 安全性vs完整性

保密性与完整性的区别

• 保密性：通过加密技术防止被动窃听者获取通信内容。其目标是确保消息的内容不被未经授权的人知晓。
• 完整性：确保消息在传输过程中未被篡改或伪造。这不仅涉及消息内容的正确性，还涉及消息来源的真实性

4.1.2 加密与消息认证

加密与消息认证的区别

• 加密：用于实现保密性，即防止未经授权的第三方获取消息内容。
• 消息认证：用于保证消息的完整性和来源的真实性，确保消息未被篡改且确实来自声称的发送者。

常见误区：许多人错误地认为加密可以自动提供消息认证，但实际上加密并不保证消息的完整性，除非它被专门设计为具有此功能。

• 使用流密码加密
  流密码加密机制：使用共享密钥生成伪随机序列（pad），然后通过与明文进行异或运算生成密文。
  漏洞分析：流密码加密的密文很容易被篡改。攻击者可以通过翻转密文中的任意一位来翻转解密后明文中的对应位。例如：
  如果用户加密了一个表示转账金额的数字（如1000美元），攻击者可以通过翻转最低位来改变金额为1001美元，或者通过翻转第11位来增加超过1000美元。
  即使攻击者不知道具体的金额，但如果有部分先验知识（如金额小于1000美元），他们可以预测修改的效果。
  结论：这种攻击并不违反加密的保密性，但它严重破坏了消息的完整性。

• 使用分组密码加密
  分组密码加密机制：使用分组密码（如AES）对数据块进行加密。
  漏洞分析：
  ECB模式：翻转密文中某个数据块的某一位只会改变解密后该数据块的对应位，其他数据块保持不变。虽然对单个数据块的影响可能难以预测，但这种局部篡改可能已经足够造成损害。此外，攻击者可以通过重新排列密文块来重新排列明文块，或者通过丢弃密文块来截断消息。
  CBC模式：攻击者可以通过翻转$IV$的某一位来改变第一个明文块的对应位，而其他明文块保持不变。
  结论：即使使用更复杂的分组密码加密模式，攻击者仍然可以通过对密文进行局部修改来实现对明文的篡改。

4.2 MAC定义

MAC的目的是防止对手修改一方发送给另一方的消息，或注入新消息，而接收方无法察觉消息并非来自预期的发送方

MAC的两个典型应用场景

• 确保两方通信时的完整性（如用户与银行之间的通信）
• 或一个用户随时间“与自己”通信（如涉及网络Cookie的情况，或用户保护其硬盘内容的情况）

消息认证码的语法

密钥生成算法 Gen：输入安全参数$1^n$，输出密钥 k，且$∣k∣≥n$。
标签生成算法 Mac：输入密钥 k 和消息 m，输出标签 t。
验证算法 Vrfy：输入密钥 k、消息 m 和标签 t，输出验证结果（1 表示有效，0 表示无效）。

要求：对于所有密钥 k 和消息 m，必须满足$Vrfy_k​(m,Mack​(m))=1$。

• 规范验证
  对于确定性的MAC，进行验证的规范方法：
  重新计算标签并检查其是否相等。换句话说，$Vrfy_k（m，t）$首先计算$\bar t：=Mack(m)$，然后输出1当且仅当$\tilde t=t$。

MAC安全

两个定义假设：

1. 攻击者可以反复请求其选择的任何消息的标签。
2. 如果攻击者能够为任何之前未认证的消息生成有效标签，则认为方案被破解。

如果无法被上述方式破解，那么MAC被称为在自适应选择消息攻击下存在性不可伪造的。

• 定义是否过于严格？
  有人提议说定义安全性时只关注有效消息就可以，但在实际中，是否有效取决于具体情况，只有严格的定义才能适应更广泛的情况。

• 重播攻击
  攻击者简单地重新发送之前已认证的消息及其有效标签。MAC本身无法防止这种攻击，因为验证过程是无状态的（即每次呈现有效的消息和标签对时，验证算法总是输出1）。
  防止方法：序列号、时间戳

• 强不可伪造性
  要求攻击者无法为任何消息生成新的有效标签，即使该消息之前已被认证过。

• 验证查询
  这些定义中的攻击者被赋予对MAC预言机的访问权限，这对应于现实世界中能够影响诚实发送方为某些消息生成标签的攻击者。

• 潜在的定时攻击
  一种测信道攻击：它需要访问验证预言机以及测量比较i和i+ 1字节所需时间差异的能力。

5.选择密文攻击(CCA)安全和认证加密

概念：攻击者选择密文让接收者解密。
简单举例：战争中，美军曾向日军透露包含AF的加密信息，通过日军的反应，可以猜测AF所代表的明文是什么。

攻击常发生在Web服务器上，用来获取TLS会话内容

5.2Padding-Oracle Attacks（填充提示攻击）

• 常用填充方式PKCS #7:
  设分组密码的分组长度为L，若密文差b个字节达到L的整数倍，那么便填充b个值为b的十六进制数
  如：差4个字节就填充0x04040404
  如果b等于0，那么便令b为L，即$b\in [1,L]$
  验证方法： 先读取最后一个字节的值b，再判断最后b个值是否都为b。

攻击方法：(CBC模式)

已知：$IV,c_1,c_2$
1.求b：
先修改最后一个块的第一个字节，如果报错，说明b=L,，否则b<L，接着修改下一个字节，重复此过程便能求出b。
2.求除填充外的最后一个明文字节：

• 设$i\in[0,2^8),$取一个
  $\Delta i$
  $=0x00,…,0x00,0xi, 0x(b+1),…,0x(b+1)$
  $\oplus,0x00,…,0x00,0x00,0xb,…,0xb$

  ps:$0xi$后跟的是b个0xb+1

• 取$c_1’=c_1\oplus \Delta i$，将$IV,c_1’,c_2$送给解密服务器
• 遍历$i$，知道服务器返回解密成功，此时的$m_2$明文形式为：
  $m_2=…;0x(b+1);0x(b+1);…;0x(b+1)$，共$b+1$个$0x(b+1)$
• 设最后一个明文非填充字节为M，则有$0x(b+1)=M\oplus i$
• 得到$M=i\oplus 0x(b+1)$
• 以此类推便可以求出所有明文字节，据我理解，求$m_1$时可以去掉$c_2$，将b最开始当作0，将$c_1,IV$发送给解密服务器。

验证码攻击

• Web服务器$S_w$（生成密文），验证码服务器$S_c$（生成验证码），两服务器共享密钥，用户$u$
  正常过程： $S_w$生成密文发送给用户$u，u$将其发送给$S_c$，$S_c$会对填充错误的密文返回错误，让$S_c$生成扭曲的验证码返回$u，u$通过查看验证码得到明文$m$，发送给$Sw$，验证通过
  攻击过程： $S_w$行为不变，$u$使用Padding Oracle Attacks去攻击$S_c$，最后得到明文$m$，此时自动脚本也能完成人机验证。

CCA安全性定义

威胁模型：

• 拥有加密预言机（黑盒，密钥随机），解密预言机，但对给定密文没有解密权限。（一般是最坏假设）
  安全目标：
• 给定攻击者一个密文$c$，若他能以显著大于$\frac12$的概率判断是$m_0,m_1$中的哪个的加密结果，则方案不安全。

5.2认证加密（AE）

目标： 保密性，完整性
保密性：CCA安全
完整性：不可伪造性
定义：如果一个私钥加密方案既是CCA安全的，又是不可伪造的，则它是一个认证加密（AE）方案。

6.哈希函数和应用

概念： 一种将长输入字符串映射到短输出字符串（摘要）的函数。
碰撞： 两个不同输入产生相同摘要。
抗碰撞性： 任何概率多项式时间算法都难以找到H中的碰撞。
带密钥的hash函数： 此时函数H有两个输入，$key:s,string:x$，输出为$H^s=H(s,x)$。其中$s$在上标是为了说明，$s$不是保密的，即使对手获得了$s$，函数H仍然具有抗碰撞性。

实际应用中基本上还是使用不带密钥的hash函数。

第二原像抗碰撞性： 已知H和x，ppt对手难以找到$x_1\neq x$，使$H^s(x_1)=H^s(x)$

抗碰撞性的hash函数也是抗第二原像碰撞的，抗第二原像碰撞的也是抗原像碰撞的。

原像抗性： 已知H和y（y=H(x)），ppt对手能找到一个$x_1$（无论是否等于x）使得$H^s(x_1)=y$。

原像抗性基本上意味着$H^s$的单向性。

6.2The Merkle-Damgard Transform

简要： $Merkle-Damgard$变换，即MD变换，是一种将定长哈希函数转换成全功能（可变长度）哈希函数的技术。
定长哈希：MD5、SHA-256等。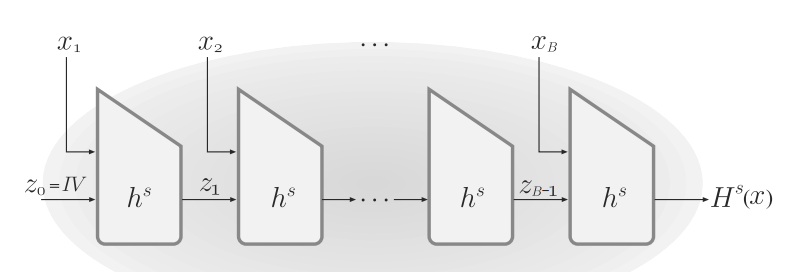

变换步骤：

• 将数据分割成多个固定大小的块，每个块大小通常等于定长哈希函数的长度
• 设置$IV$
• 对每个块进行压缩。（使用定长hash函数将前一个压缩结果和当前块进行压缩）
• 最后得到的最后一个压缩输出便是该全功能hash函数的输出

6.3 Hash-and-MAC和HMAC

6.3.1 Hash-and-MAC

实现： 首先使用Hash函数对消息进行摘要，然后使用密钥对哈希值进行签名，得到MAC

特点：

• 简单高效
• 安全可靠
  限制：
• 密钥管理
• 单向性

6.3.2 HMAC

使用hash运算的消息认证码MAC
构造：

• 对密钥进行预处理，使其与哈希函数的输入长度相同（通常是哈希函数的块长度）。
• 将经过预处理的密钥与消息进行异或运算，得到新的输入。
• 对新的输入使用哈希函数进行多轮迭代计算，得到消息认证码。

优点：

• 安全性高
• 灵活性强

6.4.1 生日攻击

介绍： 在一个大小为N的输出空间中，遍历$\Theta(\sqrt N)$时找到碰撞的概率为$\frac12$左右。

若$N=2^l$，则$\Theta(\sqrt N)=\Theta(2^{\frac12})$

有意义碰撞：

条件同上，遍历两组$\Theta(2^{\frac12})$的不同消息。
两组消息存在碰撞的概率也为$\frac12$左右。

6.4.2 小空间生日攻击

使用Floyd循环查找算法，使成功概率和运行时间与原版大致相同，但只需常数内存。

如果练过算法题，应该会知道快慢指针法，其实本质是一样的，慢指针做一次运算，慢指针做两次运算，如果有循环，总会相遇。

步骤：

• 首先选择一个随机的消息$x_0$，赋值$x:=x_0,x’:=x_0$
• 在第$i$次迭代时比较$x_i=H(x_{i-1})和x_i’=H(H(x_{i-1}’))$的值
• 如果$x_i = x_i’$，说明发生了冲突。
• （直接碰撞）且如果$x_{i-1}\neq H(x_{i-1}’)$，则冲突对为$x_{i-1}\neq H(x_{i-1}’)$
• （间接碰撞）而如果$x_{i-1} = H(x_{i-1}’)$，则说明碰撞可能发生在更早的步骤中。但由于hash值没有被记录，因此还需要再次迭代
• 存储找到的编号$i$，并将$x=x_0,x’=x_0$，重置初始值为$x_0$
• 迭代到$i$,在每一步$j$中，检查$H(x_j)=H(x_j’)$
• 若找到，则找到了碰撞，返回$x_j$和$x_j’$
• 否则，令$x_j=H(x_j)$和$x_j’=H(x_j’)$
  代码实现:

import hashlib
import random

def random_binary_string(length = 16):
	return ''.join(random.choice('01') for _ in range(length))

def H(x):
	return hashlib.sha256(x.encode()).hexdigest()

def SmallSpaceBirthdayAttack():
	x_0 = random_binary_string()
	x = x_0
	x_1 = x_0
	i = 0

	#寻找碰撞
	while True :
		x = H(x)
		x_1 = H(H(x_1))

		if x == x_1:
			break
		else:
			i += 1

	#回溯，寻找具体碰撞点
	x = x_0
	x_1 = x_0

	for j in range(i):
		if H(x) == H(x_1):
			return (x,x_1)
		else:
			x = H(x)
			x_1 = H(x_1)
	return None

ans = SmallSpaceBirthdayAttack()
if ans:
	print(ans)
else:
	print("NO！！！")

有意义碰撞

实现思想： 将两个类型不同的可选择句子映射为二进制，便可以使用上边的算法
映射方法： 例如找两个语义相反的句子，
$type 0: Alice is a good/great and honest/trustworthy worker/employee.$
$type 1: Alice is a bad/lousy and annoying/irritating worker/employee.$
将类型0/1映射到二进制的首数字，剩下的按照每个类型中的每个可选单词是选的第一个还是第二个来映射，如
$g(0000) = Alice is a good and honest worker.$
$g(1101) = Alice is a lousy and annoying employee.$

6.4.3 时空折中攻击（Hellman’s time/space tradeoff.）

时间/空间折中：通过预处理和存储，可以在存储空间和计算时间之间进行权衡，从而在合理的时间和空间复杂度内找到哈希函数的预像。

Hellman 的时间/空间折中

方法：Hellman 提出了一种更通用的时间/空间权衡方法，适用于任意函数H。

步骤：

1. 选择参数：选择参数$s$和$t$。

2. 生成表：选择$s$个均匀随机的起始点$SP_1​,…,SP_s​∈{0,1}^ℓ$。对于每个起始点$SP_i$​，计算对应的终点$EPi​:=H^{(t)}(SP_i​)（即H的t次迭代）$。

3. 存储：将所有对$(SP_i​,EP_i​)$存储在表中，按终点排序。

4. 在线阶段：给定$y$，检查$y,H(y),…,H^{(t−1)}(y)$是否与表中的某个终点匹配。如果找到匹配，则计算$H^{(t−j−1)}(SP_i​)$并检查是否为$y$的原像。

9.数论与密码困难假设

9.1.1质数和可除性

命题1： 对正整数a，b，有唯一q，r满足$a=qb+r$，其中$r\in[0,b)$
命题2： 正整数a，b，存在整数X，Y，满足$Xa+Yb=gcd（a，b）$，其中$gcd(a,b)$是这种形式能够表示的最小正整数。
命题3： 如果$c|ab，gcd(a,c)=1$，则有$c|b$
命题4： 如果$a|N,b|N,并且gcd(a,b)=1，则ab|N$

9.1.2模运算

命题： 对整数b，N，其中$b\geq 1$并且$N>1$。当且仅当$gcd(b,N)=1$时b关于N可逆。

9.1.3群

定义： 群是由集合G和二元运算$\circ$组成。

• 闭合性： 对于g，h$\in G$，$g\circ h \in G$
• 存在单位元： 存在e，使$e\circ g = g = g\circ e$
• 存在逆元： 存在h，使得$g\circ h = h\circ g = e$
• 结合性： $(g_1\circ g_2)\circ g_3 = g_1 \circ (g_2 \circ g_3)$
  阶：若元素数有限，称群为有限群，用|G|表示群的阶。
  Abelian群： 具有交换性，即满足$g\circ h = h\circ g$的群。
  子群： 如果群$H\subseteq G$ ，且H与G运算相同，则H是G的子群。
  平凡子群： G或{1}（类比平凡因子）

定理： 已知$N=\Pi_ip_i^{e_i}，其中e_i\geq 1$，则有$\phi(N)=\Pi_ip_i^{e_i-1}(p_i-1)$

9.1.4 乘法群：欧拉函数

定理： 设$N>1$是一个整数。那么$Z^*_N$是关于模$N$的乘法运算的一个阿贝尔群。
定理： 设$N=\Pi _ip_i^{e_i}$，其中${p_i}$是不同的素数，$e_i\geq 1$。那么$\Phi(N)=\Pi _ip_i^{e_i-1}(p_i-1)$

推论： 取任意整数$N>1$和$a\in Z^*_N$。则$a^{\Phi(N)}=1 \mod N$

9.1.5中国剩余定理（CRT）

已知N=pq，求$x\mod m$，令$m_1m_2=M$
$x\equiv a \mod m_1$
$x\equiv b \mod m_2$
求解过程：

• 求$M_1，M_2$，其中$M_1=\frac{M}{m_1}M_2=\frac{M}{m_2}$
• 求$M_1^{-1},M_2^{-1}$，其中$M_1^{-1}\equiv M_1 \mod m_1，M_2^{-1}$同理
• 求$x\equiv aM_1M_1^{-1}+bM_2M_2^{-1} \mod M$

9.2 素数、分解、RSA

9.2.1 生成随机素数

算法构造：
从1到$3n^2$进行循环：

• 随机选择一个n-1位的二进制数$p_0$
• 将最高位设为1，得到n位数p
• 进行Miller-Rabin测试，输入为p和参数$1^n$
• 如果输出是”素数“，则返回p
  如果再尝试$3n^2$次后没有找到素数，则返回失败。

9.2.2 素性测试

Miller-Rabin 素性测试

介绍： 基于费马小定理和二次探测定理的随机化算法
二次探测定理： 对于素数p，若$x^2\equiv 1 \mod p$，则小于p的解只有两个，$x_1=1,x_2=p-1$
步骤：

• 令$n-1=2^kq$，其中$k>0,q$为奇数，随机选取整数$a,1<a<n-1$
• 若$a^q\mod n=1$，则n有可能是素数
• 取整数$j$，$0\geq j < k$，若存在$a^{2^j}\mod n = n -1$，则n有可能是素数；否则，n为合数

定理： 如果N是奇数，且不是素数的幂，那么在$Z^*_N$中，至少有一半的元素是N是合数的强见证。

9.2.3 分解假设

因式分解假设是指存在一个相对的GenModulus，使得因式分解变得困难，其中GenModulus是一个用来生成$(N,p,q)$多项式时间算法

9.2.4 RSA假设

假设存在一个GenRSA算法，使得RSA问题在多项式时间内难以解决。这一假设是RSA公钥密码学安全性的基础。
e的选择： 最常见的选择为65537，像是e=3等容易遭受低加密指数攻击

9.3循环群中的密码学假设

9.3.1循环群和生成元

命题9.55： 设G是一个阶为 m 的有限群，且$g\in G$的阶为i，则$i|m$
推论9.56： G是一个阶为素数p的群，则G是循环群。且G中除了单位元之外所有元素都是生成元。
定理9.57： 如果p是一个素数，那么$Z_p^*$是一个阶为p-1的循环群

9.3.2离散对数/Diffie-Hellman假设

离散对数问题： 在一个循环群$G$中，给定群的生成元$g$和一个群元素$h$，求解整数$x$，使得$g^x=h$

当群的阶数较大时，这是一个十分困难的问题

Diffie-Hellman问题：

• 计算Diffie-Hellman问题（CDH）：给定$h_1=g^{x_1}和h_2=g^{x_2}$，计算$g^{x_1x_2}$
• 决策Diffie-Hellman问题（DDH）：给定$h_1=g^{x_1}和h_2=g^{x_2}和h_0$和，判断$h_0和g^{x_1x_2}是否相等$

使用素数阶群

原因： 离散对数问题在这种群中最为困难

9.3.3 $Z_p^*$的子群

定理9.66： 令p=rq+1，其中p，q为素数。则有
$$ G={[h^r\mod p]h\in Z_p^*} $$

是一个$Z_p^*$的q阶子群。

9.3.4椭圆曲线

常规表示（Weierstrass表示）：

$$ y^2=x^3+Ax+B \mod p $$

不同曲线的计算方法不一样

Montgomery表示

$$By^2=x^3+Ax^2+x \mod p$$
其中，$B\neq0\mod p且A\equiv ±2\mod p$
相比Weierstrass形式的优势： 蒙哥马利表示在某些情况下比魏尔斯特拉斯表示更高效，特别是在实现级安全性（如抵抗侧信道攻击）方面。

（Twisted) Edwards表示

$$ ax^2+y^2=1+dx^2y^2 \mod p $$
命题9.7： p是$\geq 5$的素数，E是曲线$y^2=x^3+Ax+B \mod p$

选择椭圆曲线群

实际问题

1.点压缩

在椭圆曲线中，一个点通常由两个坐标$（x, y）$表示。为了减少表示点所需的比特数，可以使用点压缩技术。

2.射影坐标

仿射坐标：点P在椭圆曲线上的表示形式为 $(x, y)$。
射影坐标：点P在射影坐标中的表示形式为 $(X, Y, Z)$，满足$X/Z=xmodp$和 $Y/Z=y\mod p$。

• 无穷远点O：在射影坐标中表示为$(0, Y, 0)$，其中$Y\neq0$。
• 转换：从仿射坐标$(x, y)$转换为射影坐标$(x, y, 1)$；从射影坐标$(X, Y, Z)$转换为仿射坐标$(X/Z\mod p,Y/Z\mod p)$。
  优势： 在射影坐标中，点的加法操作不需要计算模p的逆元。计算逆元的代价较高，而加法和乘法的代价较低

3.常用椭圆曲线

• P-256(secp256r1)： 定义在256位素数$p=2^{256}-2^{224}+2^{192}+2^{96}-1$上
  $y^2=x^3-3x+B \mod p$，其中$B$是特定常数
• P-384和P-521： 与P-256类似，p分别为384位和521位素数
• Curve25519： 定义在素数$p=2^{255}-19$上
  可以用蒙哥马利形式表示，也可以用扭曲爱德华兹形式表示（称为Ed25519）。
• secp256k1： 定义在素数$p=2^{256}-2^{32}-2^9-2^8-2^7-2^6-2^4-1$
  是一条Koblitz曲线，方程为$y^2=x^3+7\mod p$

11.密钥管理和公钥革命

11.1密钥分配和密钥管理

私钥加密三个问题：

• 密钥分配
• 存储和管理大量密钥：一个典型的解决方案是将密钥存储在安全硬件上
• 私钥加密在开放系统中的不适用性

11.2部分解决方案：密钥分配中心（KDC）

找一个守信任的实体充当KDC，帮助所有员工共享成对密钥
优点：

• 每个员工只需要存储一个长期密钥（与KDC共享）。（KDC需要存储许多长期密钥，但可以集中放在安全的地方）
• 新员工加入时，只需要新员工和KDC之间更新密钥。

缺点：

• 对KDC的成功攻击会导致系统完全崩溃。
• KDC是一个单点故障，如果宕机，安全通信将暂时无法实现，负载较高。（一种解决方法是复制更多的KDC）

使用KDC进行密钥分发的协议

Needham-Schroeder 协议，它是 Kerberos 的核心，Kerberos 是一种重要且广泛使用的用于执行身份验证和支持安全通信的服务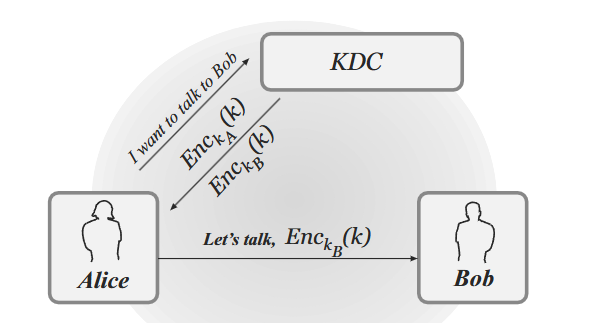

11.3密钥交换和Diffie-Hellman协议

KDC协议在实践中仍然不能解决密钥分发问题

Diffie-Hellman密钥交换协议允许两个当事人，Alice和Bob，在事先没有交换任何秘密信息的情况下达成一个秘密密钥，该方法基于循环群。

安全的设定和定义

Diffie-Hellman密钥交换协议

该协议本身基于群$Z_p^*$，其中$p$是大素数。在Diffie-Hellman（DH）密钥交换中可以使用的素数是标准化的—也就是说素数$p$必须是安全素数，即$p=2q+1$，其中$q$也是素数。

注意：自$p=2q+1$以来，素数$q$可以整除$p−1$，因此群$Z_p^∗​$有一个阶为$q$的元素$g$，$g$的幂生成群$⟨g⟩:={0,1,⋯,q−1}$。结果，这个群$⟨g⟩$是群$Z_p^∗​$的子群。

过程：

• Alice随机选择一个均匀的$a←_R​Z_q​$，即$a\in [0,p-1]$并计算$A:=g^a$。同样，Bob选择一个均匀的$b←_R​Z_q​$并计算$B:=g^b$。

• 然后，Alice和Bob交换他们各自计算出的值：Alice从Bob那里获得$B$，Bob从Alice那里获得$A$。

• 现在，Alice计算$B^a=(g^b)^a=g^{ab}$，Bob计算$A^ b=(g^a)^b=g^{ab}$，这样双方已经到达了相同的密钥$k:=g^{ab}$！

• 即使攻击者知道了$g^a和g^b$，他也无法算出$g^{ab}$，因为如果想的到这个密钥，他必须求解离散对数问题

变量	Alice	Bob	Eve
$p$	known	known	known
$q$	known	known	known
$g$	known	known	known
$a$	known	unknown	unknown
$b$	unknown	known	unknown
$g^a$	known	known	known
$g^b$	known	known	known
$g^{ab}$	known	known	unknown

活跃对手

活跃对手这里主要指，主动的攻击者，也就是说攻击者不再是简简单单的监听，而会进行中间人攻击，而Diffie-Hellman协议对于此种攻击完全没有安全性。
因此实践应用中要结合签名进行身份认证。

11.4公钥革命

数字签名（MAC对应物）：
使用私钥进行签名，使用公钥进行认证

公钥密码如何解决了私钥密码的局限性：

• 允许在公共通道进行密钥分发
• 减少了存储密钥的成本，不需要再秘密存储大量密钥
• 更加适合开放环境，便于之前没有联系的两方建立安全通信

为什么要研究私钥密码学？

私钥密码比公钥密码的效率更高，更适合大量消息的交换。

12.公钥加密

12.1概述

与私钥加密的对比

公钥加密优势（与前面类似）：

• 解决了密钥分发问题
• 便于除了一个接收方和多个发送方之间的信息传输
• 不需要知道潜在的发送方的数量和身份，具有开放性

公共密钥的安全分发

安全共享的前提是经过认证

12.2 定义

12.2.1 针对选择明文攻击的安全性

命题： 如果一个公钥加密方案在一个窃听者存在的情况下具有不可区分的加密，这个放啊便是CPA安全的。

选择明文攻击：

• 高效的对手Eve被给予公钥$pk$，并可以使用它来加密她选择的$q$条消息$m_1​,…,m_q​$以获得相应的密文$c_1​,…,c_q​$
• 如果对于任何两个消息$(μ0​,μ1​)$，由$Gen$生成的公钥$pk$和密文$c:=Enc(pk​,⋅)$（它是$μ0​$或$μ1​$的加密），Eve猜测$c$属于$μ0​$或$μ1​$的概率最多只是微不足道地大于$\frac 1 2$，则公钥加密方案$(Gen,Enc,Dec)$是CPA安全的。

公钥的不安全性

由于公钥加密的方案特性，每个攻击者都会十分容易获得加密预言机，也就是说任何确定性的公钥加密都是不具有CPA安全性的。
因此若想保证CPA安全必须使用非确定性的公钥加密，如每次加密前都进行随机填充。

12.2.2 多消息加密

定理12.6： 如果说一个加密方案$\Pi$是CPA安全的，那么它也具有不可区分的多消息加密特性

加密任意长度消息

思路：
将长消息分解为多个消息，分别加密后再组合起来，如果原始方案是CPA安全的，那么新方案也是CPA安全的。

12.2.3 针对选择密文攻击的安全性

CCA攻击方案：

• 修改发送者发送的密文$c$变为$c_0$（如修改”收件人”等固定的地方），然后再从接收者的反应行动推测明文$m$的一些内容
• 修改密文$c$变为$c_0$，其中把发送人改为自己，后续可能收到回信，从而得到明文$m_0$的一些信息。

12.3混合加密和KEM/DEM范例

主要思想：

• 发送方：使用$pk$加密私钥密钥$k$得到$c$，使用$k$加密明文$m$得到$c_1$，全部发送给接收方
• 接收方：使用$sk$解密$c$的到密钥$k$，再使用$k$解密$c_1$得到明文$m$

封装操作，一次性完成上面操作
KEM（Key Encapsulation Mechanism）：
KEM负责安全地传输对称密钥，确保只有接收方能够获取对称密钥。

• 发送方使用接收方的公钥$pk$将对称密钥$k$封装成一个密文$c$。
• 接收方使用自己的私钥$sk$从密文$c$中解封装出对称密钥$k$。

DEM（Data Encapsulation Mechanism）：
DEM负责高效地加密和解密数据，利用对称加密的高效性。

• 发送方使用对称密钥$k$对明文$m$进行加密，得到密文$c1​$。
• 接收方使用对称密钥$k$对密文$c1​$进行解密，得到明文$m$。

12.3.1 CPA安全

如果KEM是CPA安全的，且私钥加密方案（DEM）符合基本的安全性，那么混合加密方案也是CPA安全的

12.3.2 CCA安全

如果KEM是CCA安全的，且私钥加密方案（DEM）也是CCA安全的，那么混合加密方案也是CCA安全的

12.4 基于CDH/DDH的加密

12.4.1 El Gamal加密

密钥生成：

• Alice使用生成元$g$得到一个阶为$q$的循环群$G$
• 随机均匀选择一个$x\in [1,q-1]$计算$h:=g^x$
• 公开公钥$(G,q,g,h)$，保留$x$作为私钥
  加密算法：
• Bob随机均匀选择$y\in [1,q-1]$，计算密文$c_1:=g^y$
• 计算共享秘密$s:=h^y$
• 计算$c_2:=ms$
• 将密文$(c_1,c_2)=(g^y,mh^y)=(g^y,m(g^x)^y)$

  如果一个人知道了m，那么它很容易就能知道$h^y$的值。因此对每一条信息都产生一个新的$y$可以提高安全性。所以$y$也被称作临时密钥

解密算法：

• Alice计算共享秘密$s:=c_1^x$
• 计算$m=c_2s^{-1}$

实施问题

• 共享公钥参数
• 组别选择
• 消息空间

基于El Gamal的KEM构造
Gen（密钥生成）：

• 输入安全参数$1^n$，运行群生成算法$G(1^n)$，得到群$G、阶q和生成元g$。
• 随机选择一个私钥$x∈Z_q$​，计算公钥$h=g^x$。
• 定义一个函数$H:G→{0,1}^ℓ$，其中$ℓ$是某个函数的值。
• 公钥为$(G,q,g,h,H)$，私钥为$(G,q,g,x)$。

Encaps（封装）：

• 输入公钥$pk=(G,q,g,h,H)$。
• 随机选择$y∈Zq_​$，计算密文$c=g^y$。
• 计算对称密钥$K=H(h^y)$。
• 输出密文$c$和对称密钥$K$。

Decaps（解封装）：

• 输入私钥$sk=(G,q,g,x)$和密文$c∈G$。
• 计算$cx=(g^y)^x=g^{xy}$。
• 计算对称密钥$K=H(g^{xy})$。
• 输出对称密钥$K$。

ps：其中$H$应为一种理想化的Hash函数

CDH是一个计算问题，要求计算出具体的共享密钥$g^{ab}$。
DDH是一个决策问题，要求判断一个给定的群元素是否是两个其他群元素的“组合”

12.4.2 基于DDH的密钥封装

定理： 如果DDH（决策性Diffie-Hellman）问题在群G中是困难的，并且H按照上边方式选择，那么这种构造是一个CPA安全的KEM

12.4.3 基于CDH的随机预言模型中的KEM

CDH假设：CDH假设表明，给定$g^x$和$g^y$，计算$g^{xy}$是困难的。
定理： 如果CDH问题是困难的，并且 H 被建模为随机预言，那么Construction 12.19是CPA安全的

12.4.4 选择密文安全性和DHIES/ECIES

定理： 如果假设$gap-CDH$问题是困难的，那么KEM可以实现CCA安全
gap-CDH假设：
Gap-CDH假设是CDH问题的一个更强版本，它假设即使攻击者可以访问一个解决DDH问题的预言机，CDH问题仍然是困难的。换句话说，即使攻击者可以判断$g^x$和$g^y$是否与$g^{xy}$有关，他们仍然无法计算$g^{xy}$。

DHIES/ECIES方案：
这是一个CCA安全的加密方案，结合KEM和私钥加密方案（如CPA安全的对称加密方案）以及MAC。
Gen：

• 输入安全参数$1^n$，允许群生成算法$G(1^n)$，得到群$G$、阶$q$和生成元$g$
• 随机选择$x\in Z_q$，计算$h=g^x$
• 定义一个函数$H：G\to {0,1}^{2n}$
• 公钥${G,q,g,h,H}$，私钥为$x$

Enc：

• 输入公钥$pk=(G,q,g,h,H)$和消息$m$
• 随机选择$y\in Z_q$，计算$k_E||k_M=H(h^y)$，其中$k_E$是对称加密密钥，$k_M$是MAC密钥
• 使用对称加密方案$\Pi E$加密消息$m$，得到$c_0=Enc{k_E}(m)$
• 计算MAC值$t=Mac_{k_M}(c_0)$
• 输出密文$(g^y,c_0,t)$

Dec：

• 输入私钥$sk=(G,q,g,x,H)$和密文$(c,c_0,t)$
• 检查$c\in G$，如果$c\notin G$，返回$\perp$
• 计算$k_E||k_E=H(c^x)$
• 验证MAC值$Vefy_{k_E}(c_0,t)$。得到消息$m=Dec_{k_E}(c_0)$

DHIES/ECIES:

• DHIES：当群$G$是有限域的循环子群时，这种构造被称为DHIES。
• ECIES：当群$G$是椭圆曲线群时，这种构造被称为ECIES。

12.5基于RSA的加密

12.5.1 普通RSA加密

普通RSA中的更多攻击

• m恢复效率提升两倍
  明文分解：假设$m$是一个均匀的$n$位整数，那么对于适当的$α≈\frac 12$​，可以证明以高概率存在整数$r$和$s$，使得$1<r≤s≤2^{αn}$且$m=rs$

攻击过程：
1.计算$x_r​=cr^{−e} \mod N$，这实际上是将密文$c$除以$r^e$。
2.如果存在某个$s$使得$s^e\mod N=x_r$​，则$m=r⋅s$。
3.通过排序和二分查找，可以在$O(T)$的时间内找到这样的$r$和$s$

• 小e加密
• m部分已知
• 加密相关消息
• 向多个接收者发送相同消息

这部分内容可以看我博客CTF RSA题型

12.5.2 Padded RSA 和 PKCS#1 v1.5

随机填充的作用：随机填充$r$使得加密过程不再是确定性的，从而提高了安全性

RSA PKCS#1 v1.5

消息长度： 消息$m$的长度为$D$字节，其中$1\leq D\leq k-11$，$k$是$N$的字节长度
加密过程：

• 选择一个长为$k-D-3$字节的随机填充$r$，且$r$中没有字节等于0x00
• 填充后的消息$p=0x00||0x02||r||0x00||m$
• 计算密文$c=p^e\mod N$

缺陷：
填充长度可能太短，攻击者可通过暴力攻击恢复部分明文

12.5.3 无随机预言的CPA安全加密

本小节只进行理论上的讨论，因为实际中有更高效的构造方案

RSA问题的硬核谓词

定义：硬核谓词是一种从单向函数的输出中难以计算的特定信息。对于RSA问题，最小有效位（lsb）被证明是一个硬核谓词。

构建KEM

目标：扩展单比特加密方案，生成一个长度为$n$的密钥。
方法：通过重复应用RSA置换（即模$N$下的$e$次幂运算），从一个初始随机值$c_1​$开始，依次计算$c_1^e \mod N$，$(c_1^e​)^e\mod N$，直到$c_1^{e^n} \mod N$。最终的密文是$c_{n+1}$​，而密钥则是由这些中间值的最小有效位组成的序列。
解密过程：接收方使用私钥$d_0​=[d^n\mod ϕ(N)]$反向计算，恢复初始值$c_1$​，并从中提取密钥。
定理12.35：如果RSA问题是困难的，那么该构建是一个CPA安全的KEM

效率

加密：需要$2n$次模$N$的乘法。
解密：需要一次完整的模$N$指数运算（大约3072次模$N$的乘法）加上额外的$2n$次模$N$的乘法。

12.5.4 OAEP and PKCS #1 v2

普通RSA加密

纯RSA加密连CPA安全都无法保证，因为它是一个确定性加密方案。

RSA PKCS #1 v1.5

PKCS #1 v1.5存在一种更实用的CCA攻击，攻击者不需要完整的解密预言机，只需要一个“部分”解密预言机，该预言机指示解密是否成功。这种攻击利用了PKCS #1 v1.5在解密时对填充格式的检查。

Bleichenbacher攻击：攻击者通过选择随机的$s∈Z_N^∗​$并提交$c′=[s^e⋅c\mod N]$给解密者，利用解密者的响应来逐步恢复明文$m$。

RSA-OAEP构建

Gen：

• 输入安全参数$1^n$，允许$Gen(1^n)$，得到公钥$(N,e)$和私钥$(N,d)$
• 输出公钥$pk=(N,e)$和私钥$sk=(N,d)$

Enc：

• 输入公钥$pk=(N,e)$和消息$m\in {0,1}^l$
• 设置$m_0:=m||0^k$（即在$m$后加$k$个0）
• 随机选择$r\in {0,1}^k$
• 计算$t:=m_0 \oplus G(r)$和$s:=r\oplus H(t)$
• 设置$m_1:=s||t$
• 输出密文$c:=[m_1^e \mod N]$

Dec：

• 输入私钥$sk=(N,d)$和密文$c\in Z_N^*$
• 计算$m_1:=[c^d \mod N]$
• 解析$m_1$为$s||t$
• 计算$r:=H(t)\oplus s$和$m_0:=G(r)\oplus t$
• 检查$m_0$的最后$k$位是否全为0，如果不是，返回错误
• 否则丢弃$m_0$的最后$k$个0，输出剩余的$l$位作为消息$m$

Manger’s CPA on PKCS #1 v2.0.

Manger攻击：2001年，James Manger发现了一种针对PKCS #1 v2.0的CCA攻击，即使PKCS #1 v2.0是RSA-OAEP的一个变体。这种攻击利用了某些实现中返回不同错误信息的问题。

12.5.5 随机预言模型中CCA安全的KEM

构造

Gen

• 输入安全参数$1^n$。
• 运行RSA密钥生成算法$GenRSA(1^n)$，得到公钥$(N,e)$和私钥$(N,d)$。
• 定义一个函数$H:Z_N^∗​→{0,1}^n$，该函数在分析中被建模为随机预言。

Encaps

• 输入公钥$pk=(N,e)$。
• 随机选择$r∈Z_N^∗$​。
• 计算密文$c:=[r^e\mod N]$和密钥$k:=H(r)$。
• 输出密文$c$和密钥$k$。

Decaps

• 输入私钥$sk=(N,d)$和密文$c∈Z_N^∗$​。
• 计算$r:=[c^d\mod N]$。
• 输出密钥$k:=H(r)$。

安全性：
在CCA攻击中，攻击者可以查询解封装预言机（Decapsulation Oracle），但这些查询不会泄露关于密钥$H(r)$的任何额外信息。
解封装预言机的查询只会返回$(H)(\bar r)$，其中$\bar r=[\bar c^d\mod N]$。如果$\bar c=c$，则$\bar r=r$，但$H(r)$仍然是随机的，因为$H$是随机预言。
因此，即使攻击者可以查询解封装预言机，也无法区分挑战密文所封装的密钥$k$和一个随机密钥。

12.5.6 RSA的实现问题和陷阱

使用CRT时的故障攻击

如果在计算过程中发生错误（例如，攻击者通过硬件篡改诱导错误），可能会导致安全问题。

依赖公钥I

• 问题：多个接收者使用相同的模数$N$，但不同的公钥指数$e_i$和私钥指数$d_i$​。
• 攻击：给定$N$和$e_i​⋅d_i​=1\mod ϕ(N)$，可以高效地分$N$。一旦分解了$N$，就可以计算任何$e_j​$的逆元$d_j$​。
• 后果：任何员工都可以读取发送给其他员工的加密消息。

依赖公钥II

• 问题：即使所有员工相互信任，共享模数$N$仍然不安全。
• 攻击：假设相同的明文$m$被加密并发送给两个员工，其公钥分别为$(N,e_1​)$和$(N,e_2​)$，且$gcd(e_1​,e_2​)=1$
• 攻击方法：攻击者可以看到两个密文$c_1​=m^{e_1}​\mod N$和$c_2​=m^{e_2}​\mod N$。利用扩展欧几里得算法计算整数$X$和$Y$，使得$Xe_1​+Ye_2​=1$。那么$m=[c_1^X​⋅c_2^Y​\mod N]$。
• 后果：攻击者可以轻松恢复明文$m$

13.数据签名方案

13.1 概述

数字签名是一种公钥密码学工具，允许签名者$S$使用其私钥$sk$对消息$m$进行签名，生成签名$σ$。任何知道签名者公钥$pk$的人都可以验证签名的合法性，从而确认消息确实由签名者生成且未被篡改。

与MAC的比较

MAC局限性： 无法实现公开验证、不可抵赖性 和签名的可转移性。
数字签名优势：

• 公开验证：任何知道公钥的人都可以验证签名。
• 不可抵赖性：签名者无法否认自己对消息的签名。
• 可转移性：签名可以被第三方验证，并可进一步传递给其他方。

与公钥加密的联系

误解：数字签名有时被错误地视为公钥加密的“逆操作”，即通过私钥解密消息来生成签名，通过公钥加密签名来验证。这种观点是错误的，因为：

• 不适用性：在大多数情况下，这种方法根本不可行。
• 不安全性：即使在可以应用的情况下，生成的签名方案也不安全。
  正确关系：数字签名和公钥加密是两种不同的密码学原语，尽管它们都基于公钥密码学，但它们的设计和安全性要求不同。

13.2定义

签名方案的安全性

数字签名方案的安全性要求攻击者无法伪造签名，即使它已经获得了许多其他消息的签名。

13.3 hash签名方案

构造：
假设我们有一个签名方案$Π=(Gen,Sign,Vrfy)$，它适用于长度为$ℓ(n)$的消息，以及一个哈希函数 $Π_H​=(Gen_H​,H)$，其输出长度为 ℓ(n)。我们构造一个新的签名方案$Π′=(Gen′,Sign′,Vrfy′)$，如下所示：

Gen’：

• 输入：安全参数$1^n$。
• 运行$Gen(1^n)$生成密钥对$(pk,sk)$。
• 运行$Gen_H​(1^n)$生成哈希函数的参数$s$。
• 公钥为$⟨pk,s⟩$，私钥为$⟨sk,s⟩$。

Sign‘：

• 输入：私钥$⟨sk,s⟩$和消息$m∈{0,1}^∗$。
• 计算哈希值$H_s​(m)$。
• 使用私钥$sk$对哈希值$H_s​(m)$进行签名，得到签名$σ←Sign_{sk}​(H_s​(m))$
• 输出签名$σ$。

Vrfy’

• 输入：公钥$⟨pk,s⟩$、消息$m∈{0,1}^∗$和签名$σ$。
• 计算哈希值$H_s​(m)$。
• 使用公钥$pk$验证签名$σ$是否是$Hs​(m)$的有效签名，即检查$Vrfy_{pk}​(H_s​(m),σ)=1$。
• 如果验证通过，输出1（有效）；否则输出0（无效）。

定理13.4：如果$Π$是一个安全的签名方案（适用于长度为 ℓ 的消息），并且$Π_H$是抗碰撞性的，那么上面构造就是一个安全的签名方案（适用于任意长度的消息）

13.4 基于RSA的签名

13.4.1普通RSA签名

无消息攻击

攻击者可以选择一个随机的$σ∈Z_N^∗$​，计算$m:=[σ^e\mod N]$，然后输出伪造的签名对$(m,σ)$。这种攻击是有效的，因为$σ$是$m$的有效签名。

任意消息上的签名

攻击者可以选择两个消息$m_1​,m_2​∈Z_N^∗$​，使得$m=m_1​⋅m_2 \mod N$。然后获取$m_1​$和$m_2​$的签名$σ1​,σ2$​，并输出$σ:=[σ_1​⋅σ_2 \mod N]$作为$m$的签名。这种攻击也是有效的，因为：
$σ^e=(σ^1​⋅σ_2​)^e=(m_1^d​⋅m_2^d​)^e=m_1​⋅m_2​=m\mod N$

13.4.2 RSA-FDH 和PKCS #1标准

构造：
Gen：

• 输入安全参数$1^n$。
• 运行$GenRSA(1^n)$生成模数$N$和整数$e,d$，满足$ed=1modϕ(N)$。
• 公钥为$pk=(N,e)$，私钥为$sk=(N,d)$。
• 定义一个函数$H:{0,1}∗→Z_N^∗​$

Sign：

• 输入私钥$sk=(N,d)$和消息$m∈{0,1}^∗$。
• 计算签名$σ:=[H(m)^d\mod N]$。

Vrfy：

• 输入公钥$pk=(N,e)$、消息$m$和签名$σ$。
• 验证是否$σ^e=H(m)\mod N$

RSA PKCS #1标准

• PKCS #1 v1.5：与RSA-FDH非常相似，但存在一些已知的安全性问题。
• PKCS #1 v2.1：包含一个更复杂的方案，可以视为RSA-FDH的随机化变体。

13.5离散对数问题的签名

13.5.1标识方案和签名

识别方案

识别方案是一种交互式协议，允许一方（称为“证明者”）向另一方（称为“验证者”）证明其身份。

从识别方案到签名

Fiat-Shamir变换：

• 变换方法：Fiat-Shamir变换可以将任何交互式的识别方案转换为非交互式的签名方案。
• 基本思想：签名者作为证明者，自己运行识别协议。签名者首先计算初始消息$I$，然后通过哈希函数$H$生成挑战$r$，最后计算响应$s$。签名是$(r,s)$
• 验证过程：验证者重新计算 I 并检查$H(I,m)=r$。

13.5.2 Schnorr 身份识别/签名方案

构造：

Gen：与识别方案相同。

Sign：

• 选择随机$k∈Z_q​$，计算$I=g^k$。
• 计算$r=H(I,m)$
• 计算$s=[rx+k\mod q]$。
• 输出签名$(r,s)$。

Vrfy：

• 计算$I=g^s⋅y^{−r}$。
• 检查是否$H(I,m)=r$。

安全性：如果离散对数问题是困难的，并且哈希函数 H 被建模为随机预言，那么Schnorr签名方案是安全的。

13.5.3 DSA和ECDSA

DSA构造

Gen：
运行$G(1^n)$生成群$G$、阶$q$和生成元$g$。选择随机$x∈Z_q$​，计算$y=g^x$。公钥为$(G,q,g,y)$，私钥为$x$。

Sign：

• 选择随机$k∈Z_q^∗$​，计算$r=F(g^k)$。
• 计算$s=[k^{−1}⋅(H(m)+xr)\mod q]$。
• 输出签名$(r,s)$。

Vrfy：

• 计算$I=g^{H(m)⋅s^{−1}}⋅y^{r⋅s^{−1}}$。
• 检查是否$r=F(I)$

ECDSA构造

Gen：与DSA相同，但群$G$是椭圆曲线群。

Sign：

• 选择随机$k∈Z_q^∗$​，计算$r=F(g^k)$。
• 计算$s=[k^{−1}⋅(H(m)+xr)\mod q]$。
• 输出签名$(r,s)$。

Vrfy：

• 计算$I=g^{H(m)⋅s^{−1}}⋅y^{r⋅s^{−1}}$。
• 检查是否$r=F(I)$。