NepCTF 2025 Writeup

记录一下NepCTF比赛MISC和Crypto方向的部分试题复现（有些暂时没看懂，后续有空再接着复现吧），题目还是很好的，覆盖面比较广，学到了许多知识(`・ω・´)

MISC

NepBotEvent

根据题目分析，该题所给的文件跟Keylogger有关，也就是跟键盘流量相关。
提到键盘流量分析，我们就会想到HID DATA的8字节的数据，而这个文件并不是流量数据包，因此不能够让wireshark帮我们提取出HID data，因此我们要通过二进制数据来分析出哪些数据代表着HID data。
通过搜索可以发现，其实该文件是 Linux 下常见的键盘事件数据，每组24个字节，对应 Linux input 子系统的 input_event 结构体。
该结构体定义在 /usr/include/linux/input.h：

struct timeval {
    long tv_sec;   // 8字节，秒
    long tv_usec;  // 8字节，微秒
};
struct input_event {
    struct timeval time; // 16字节
    __u16 type;          // 2字节
    __u16 code;          // 2字节
    __s32 value;         // 4字节
}

直接ai一个脚本

# exp.py
# 读取和解析Linux evdev键盘事件文件（每组24字节），恢复输入按键，同时记录shift按键的按下与松开

import struct

LINUX_KEYCODE = {
    1: '[ESC]', 2: '1', 3: '2', 4: '3', 5: '4', 6: '5', 7: '6', 8: '7', 9: '8', 10: '9', 11: '0',
    12: '-', 13: '=', 14: '[BACKSPACE]', 15: '\t', 16: 'q', 17: 'w', 18: 'e', 19: 'r', 20: 't',
    21: 'y', 22: 'u', 23: 'i', 24: 'o', 25: 'p', 26: '[', 27: ']', 28: '\n', 29: '[CTRL]',
    30: 'a', 31: 's', 32: 'd', 33: 'f', 34: 'g', 35: 'h', 36: 'j', 37: 'k', 38: 'l',
    39: ';', 40: "'", 41: '`', 42: '[LSHIFT]', 43: '\\', 44: 'z', 45: 'x', 46: 'c', 47: 'v',
    48: 'b', 49: 'n', 50: 'm', 51: ',', 52: '.', 53: '/', 54: '[RSHIFT]', 55: '[PRTSCR]',
    56: '[ALT]', 57: ' ', 58: '[CAPSLOCK]', 59: '[F1]', 60: '[F2]', 61: '[F3]', 62: '[F4]',
    63: '[F5]', 64: '[F6]', 65: '[F7]', 66: '[F8]', 67: '[F9]', 68: '[F10]', 69: '[NUMLOCK]',
    70: '[SCROLLLOCK]', 71: '[HOME]', 72: '[UP]', 73: '[PGUP]', 74: '-', 75: '[LEFT]', 76: '[CENTER]',
    77: '[RIGHT]', 78: '+', 79: '[END]', 80: '[DOWN]', 81: '[PGDN]', 82: '[INS]', 83: '[DEL]',
    87: '[F11]', 88: '[F12]', 97: '[RCTRL]', 100: '[RALT]'
    # 可继续扩展
}

SHIFT_CODES = [42, 54]  # 左右shift的keycode

def parse_evdev_event(data):
    # 结构体: struct timeval (2x8字节), type (H), code (H), value (I) 小端序
    tv_sec, tv_usec, type_, code, value = struct.unpack('<qqHHI', data)
    return type_, code, value

def keylog_restore(filename):
    result = []
    with open(filename, 'rb') as f:
        while True:
            chunk = f.read(24)
            if len(chunk) < 24:
                break
            type_, code, value = parse_evdev_event(chunk)
            # 只处理键盘事件
            if type_ == 1:
                if code in SHIFT_CODES:
                    if value == 1:
                        result.append(f'{LINUX_KEYCODE[code]}↓')
                    elif value == 0:
                        result.append(f'{LINUX_KEYCODE[code]}↑')
                elif value == 1:
                    char = LINUX_KEYCODE.get(code)
                    if char:
                        result.append(char)
    return ''.join(result)

if __name__ == '__main__':
    import sys
    if len(sys.argv) != 2:
        print('用法: python exp.py NepBot_keylogger')
        sys.exit(1)
    filename = sys.argv[1]
    output = keylog_restore(filename)
    print('恢复的键盘输入记录:')
    print(output)

输出：

通过分析我们便能够得到数据库名为NepCTF-20250725-114514。

SpeedMino

一个俄罗斯方块游戏，按照题目的意思来看只要玩够2600分就可以获得flag，但是试了一下发现还是比较费时间的，于是转换思路从源码入手。
解压SpeedMino.exe文件，得到源码，发现是lua源码，查看main.lua，搜索2600，发现了结果计算的逻辑。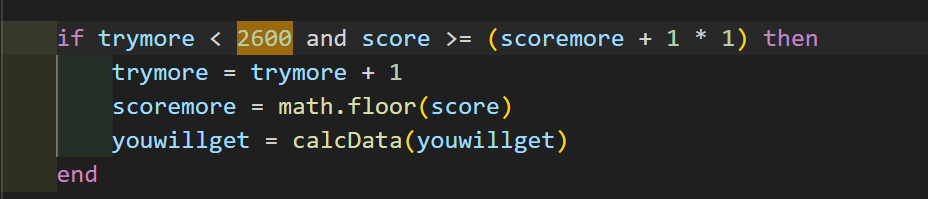

通过函数名等关键词跳转，发现所有的数据计算方法都能够在该文件中找到，直接把代码丢给ai写一个最后输出flag的计算脚本：

youwillget = [187, 24, 5, 131, 58, 243, 176, 235, 179, 159, 170, 155,
              201, 23, 6, 3, 210, 27, 113, 11, 161, 94, 245, 41,
              29, 43, 199, 8, 200, 252, 86, 17, 72, 177, 52, 252,
              20, 74, 111, 53, 28, 6, 190, 108, 47, 16, 237, 148,
              82, 253, 148, 6]

# 等价于 Lua 的 youwillget[0] = #youwillget
youwillget.insert(0, len(youwillget))

def KSA() -> list[int]:
    key = b"Speedmino Created By MrZ and modified by zxc"
    key_len = len(key)
    S = list(range(256))
    j = 0
    for i in range(256):
        j = (j + S[i] + key[i % key_len]) % 256
        S[i], S[j] = S[j], S[i]
    return S


secretBox = KSA()
secret_i = 0
secret_j = 0


def calc_data(text_table: list[int]) -> list[int]:
    global secret_i, secret_j
    K = [text_table[0]]         # K[0] = text_len
    text_len = text_table[0]
    for n in range(1, text_len + 1):
        secret_i = (secret_i + 1) % 256
        secret_j = (secret_j + secretBox[secret_i]) % 256
        secretBox[secret_i], secretBox[secret_j] = \
            secretBox[secret_j], secretBox[secret_i]
        idx = (secretBox[secret_i] + secretBox[secret_j]) % 256
        K.append((text_table[n] + secretBox[idx]) % 256)
    return K


pass_table = [55] + [32] * 55   # 长度 55，全空格
calc_data(pass_table)           # 只调用，丢弃返回值，目的是推进 i/j/S


for _ in range(2600):
    youwillget = calc_data(youwillget)


def table_to_str(text: list[int]) -> str:
    text_len = text[0]
    out = []
    for i in range(1, text_len + 1):
        c = text[i]
        if c < 32 or c >= 127:
            out.append('#')
        else:
            out.append(chr(c))
    return ''.join(out)


print("flag:", table_to_str(youwillget))

得到flag：NepCTF{You_ARE_SpeedMino_GRAND-MASTER_ROUNDS!_TGLKZ}

meowble猫泡

打开附件，发现是一个Unity游戏，打开游戏跑一下，发现有提示，跑一会儿就可以发现会给出部分flag，但是貌似并不会获得全部，我们这里可以使用一款Unity游戏数据解析工具：Downloads 来导出游戏数据。之后我们就可以使用Notepad++直接搜索提示信息Tiptext了。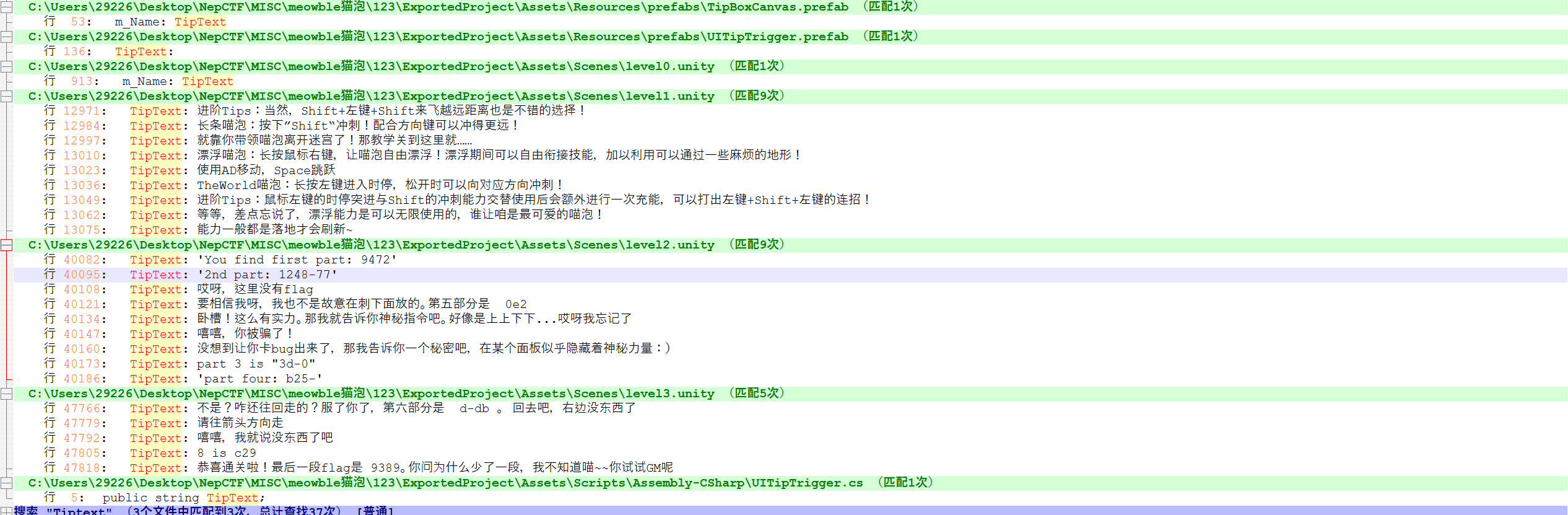

但是发现flag也是少了第7段flag，提示给出让试试GM，应该是GameManager模式，直接在Assets\Scripts目录下查看CS脚本，发现可疑脚本，猜测应该是管理gm逻辑的：

分析CS脚本就知道是gm的启动方式是“上上下下左右左右BA”（貌似是魂斗罗30条命作弊代码），直接进入游戏按下Esc之后再按下对应按键进入GM模式，让输入命令，随便输入一些字母会发现提示：

因此我们可以输入“help”来寻找获取flag的方法，然后我们就可以发现能够getflag，然后我们结合缺失的flag和getflag的用法使用getflag 7来获取flag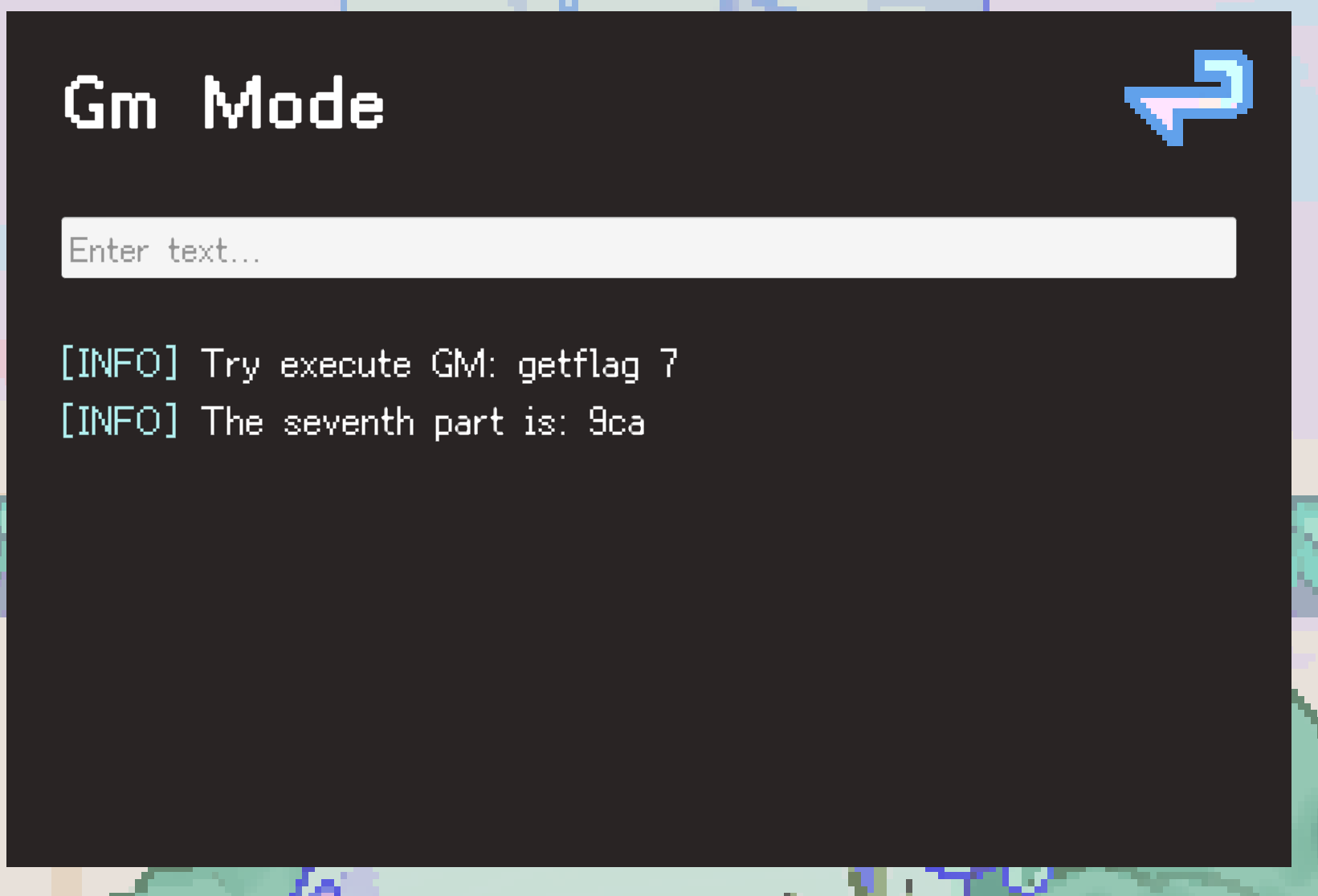

1	`NepCTF{94721248-773d-0b25-0e2d-db9cac299389}`

客服小美

题目： 一个流量包+一个内存镜像文件raw

使用ufs打开可以查看到用户名为JohnDoe，同时能够发现桌面上存在exe文件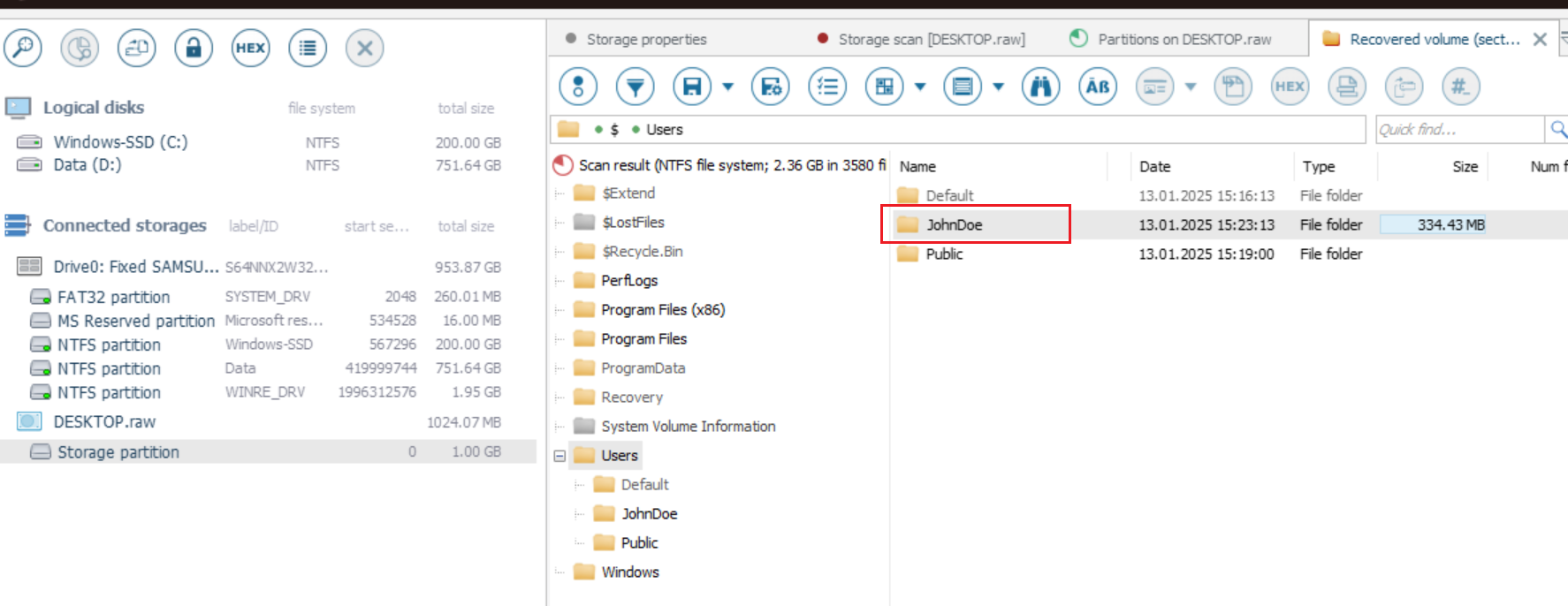

也可以使用vol2来查看

1	`vol2 -f DESKTOP.raw imageinfo`

扫描结果：

Volatility Foundation Volatility Framework 2.6.1
INFO    : volatility.debug    : Determining profile based on KDBG search...
          Suggested Profile(s) : Win10x64_19041
                     AS Layer1 : SkipDuplicatesAMD64PagedMemory (Kernel AS)
                     AS Layer2 : FileAddressSpace (/home/kali/Desktop/DESKTOP.raw)
                      PAE type : No PAE
                           DTB : 0x1ad000L
                          KDBG : 0xf8005221eb20L
          Number of Processors : 2
     Image Type (Service Pack) : 0
                KPCR for CPU 0 : 0xfffff80050626000L
                KPCR for CPU 1 : 0xffffb181d5940000L
             KUSER_SHARED_DATA : 0xfffff78000000000L
           Image date and time : 2025-01-13 07:30:02 UTC+0000
     Image local date and time : 2025-01-13 15:30:02 +0800

找到系统版本后，可以尝试继续扫描桌面信息

1	`vol2 -f DESKTOP.raw --profile=Win10x64_19041 filescan\|grep Desktop`

扫描结果如下：

Volatility Foundation Volatility Framework 2.6.1
0x0000d804abd02720      2      0 R--r-d \Device\HarddiskVolume3\Windows\System32\DispBroker.Desktop.dll
0x0000d804abd6dd30  32768      1 R--rw- \Device\HarddiskVolume3\Users\JohnDoe\Desktop
0x0000d804ac697ab0     11      0 R--r-d \Device\HarddiskVolume3\Windows\System32\SettingsEnvironment.Desktop.dll
0x0000d804ac8b1660  31802      1 RW-rw- \Device\HarddiskVolume3\Users\JohnDoe\Desktop\DESKTOP-OKEP6GL-20250113-073001.raw
0x0000d804acf0ae80     15      0 R--r-d \Device\HarddiskVolume3\Users\JohnDoe\Desktop\DumpIt.exe
0x0000d804ad57f710      1      0 R--r-d \Device\HarddiskVolume3\Users\JohnDoe\Desktop\DumpIt.exe
0x0000d804ad5806b0      5      0 R--r-d \Device\HarddiskVolume3\Windows\System32\WindowsInternal.ComposableShell.DesktopHosting.dll
0x0000d804ad581b00      4      0 R--r-d \Device\HarddiskVolume3\Users\JohnDoe\Desktop\关于2025年部分节假日安排的通知.exe

我们也可以得出用户名为JohnDoe
然后追踪一下data

1	`vol2 -f DESKTOP.raw --profile=Win10x64_19041 pslis`

找到Beacon对应进程号6492

使用Beta/cs-parse-http-traffic.py提取取流量中的raw data

1	`python cs-parse-http-traffic.py -k unknown DESKTOP.pcapng`

选取其中对44请求的回应数据

先使用vol2 -f DESKTOP.raw --profile=Win10x64_19041 memdump -p 6492 -D ./将对应Beacon进程dump下来，然后使用Beta/cs-extract-key.py来提取密钥

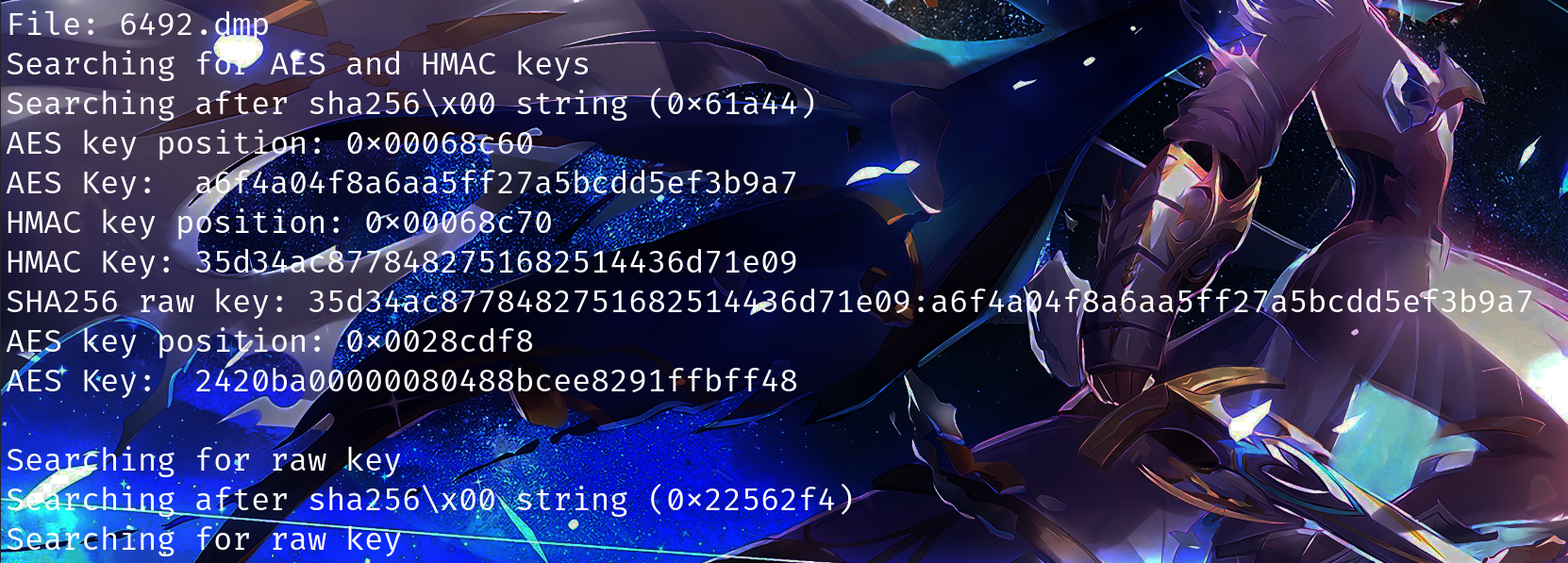
1	`python cs-extract-key.py -t 9ea8c274326a1db1e25142558f2bac154d8139bc18a19f5d772786e8075d6d8fca4d82ed8a7253e3e2c17110e911ff16 6492.dmp`

可以获得Beacon会话的主密钥

1 2	`AES Key: a6f4a04f8a6aa5ff27a5bcdd5ef3b9a7 HMAC Key: 35d34ac8778482751682514436d71e09`

然后挨个对过滤出的data进行解密，找到flag。项目地址：CS_Decrypt/Beacon_Task_return_AES_Decrypt.py at main · WBGlIl/CS_Decrypt

'''
Beacon任务执行结果解密
'''
import hmac
import binascii
import base64
import struct
import hexdump
from Crypto.Cipher import AES

def compare_mac(mac, mac_verif):
	if mac == mac_verif:
		return True
	if len(mac) != len(mac_verif):
		print
		"invalid MAC size"
		return False

	result = 0

	for x, y in zip(mac, mac_verif):
		result |= x ^ y

	return result == 0

def decrypt(encrypted_data, iv_bytes, signature, shared_key, hmac_key):
	if not compare_mac(hmac.new(hmac_key, encrypted_data, digestmod="sha256").digest()[0:16], signature):
		print("message authentication failed")
		return

	cypher = AES.new(shared_key, AES.MODE_CBC, iv_bytes)
	data = cypher.decrypt(encrypted_data)
	return data

SHARED_KEY = binascii.unhexlify("a6f4a04f8a6aa5ff27a5bcdd5ef3b9a7")
HMAC_KEY = binascii.unhexlify("35d34ac8778482751682514436d71e09")

enc = "00000050350ca7f4379f30cc9d6d671db886d360691c74467156e60e8356725ae2f3b880b302ea8b5556df10324e86e53ecb84046646a1758e9cb8c7fca42d660617be467627abcc3c0ce3bd3e93c02fffcb4d3a"
encrypt_data=binascii.unhexlify(enc)


encrypt_data_length=encrypt_data[0:4]

encrypt_data_length=int.from_bytes(encrypt_data_length, byteorder='big', signed=False)

encrypt_data_l = encrypt_data[4:len(encrypt_data)]

data1=encrypt_data_l[0:encrypt_data_length-16]
signature=encrypt_data_l[encrypt_data_length-16:encrypt_data_length]
iv_bytes = bytes("abcdefghijklmnop",'utf-8')

dec=decrypt(data1,iv_bytes,signature,SHARED_KEY,HMAC_KEY)

counter = dec[0:4]
counter=int.from_bytes(counter, byteorder='big', signed=False)
print("counter:{}".format(counter))

dec_length = dec[4:8]
dec_length=int.from_bytes(dec_length, byteorder='big', signed=False)
print("任务返回长度:{}".format(dec_length))

de_data= dec[8:len(dec)]
Task_type=de_data[0:4]
Task_type=int.from_bytes(Task_type, byteorder='big', signed=False)
print("任务输出类型:{}".format(Task_type))

print(de_data[4:dec_length])

print(hexdump.hexdump(dec))

输出得到flag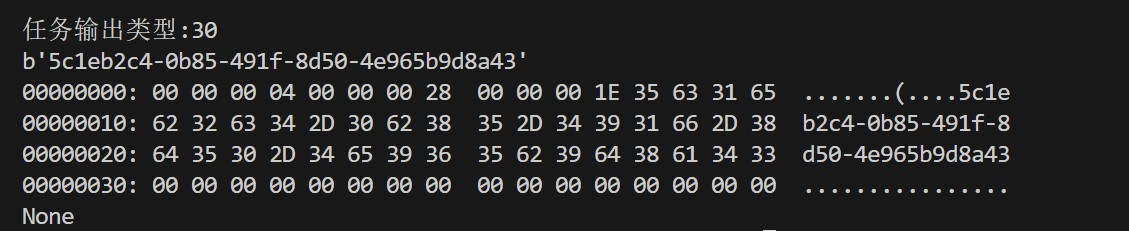

easyshock

题目：

from unicorn import *
from unicorn.x86_const import *
from capstone import *
from capstone.x86_const import *
import os
import random
from Crypto.Util.number import *
from Crypto.Cipher import ARC4

FLAG = os.getenv('FLAG','test{This_is_a_test_flag_connect_to_get_true_flag}').encode()

CODE_COUNT = 0
TARGET_COUNT = 0
# memory address where emulation starts
CODE_ADDRESS    = 0x110000
DATA_ADDRESS    = 0x220000
OUTPUT_ADDRESS  = 0x330000
KEY_ADDRESS     = 0x440000
STACK_ADDRESS   = 0x880000
CODE = b''
with open("prog","rb") as f:
    CODE = f.read()


ENTRY_POINT = CODE_ADDRESS + 0x0
ENTRY_POINT_END = CODE_ADDRESS + 0x296


def flipBit(uc:Uc,reg_name:str):
    randBit = random.randint(0,7) #not 0,63
    reg_num = eval("UC_X86_REG_" + reg_name.upper())
    reg_value = uc.reg_read(reg_num)
    reg_value ^= 1 << randBit
    uc.reg_write(reg_num,reg_value)

def shock(uc:Uc):
    rip = uc.reg_read(UC_X86_REG_RIP)
    code = uc.mem_read(rip,16)
    md = Cs(CS_ARCH_X86, CS_MODE_64)
    md.detail = True
    dis = None
    for d in md.disasm(code, 0):
        dis = d
        break
    for reg_list in dis.regs_access():
        for reg in reg_list:
            flipBit(uc,md.reg_name(reg))


def hook_code(uc:Uc, address, size, user_data):
    global CODE_COUNT
    if(CODE_COUNT >= 199999):
        print("   [⏰] Time Limit Exceed")
        uc.emu_stop()
    if(CODE_COUNT == TARGET_COUNT):
        print("   [⚡] Shock!")
        shock(uc)
    CODE_COUNT += 1

def run(data,key,target):
    # print("   [🔒] to enc: ",data.hex())
    try:
        global CODE_COUNT
        global TARGET_COUNT
        CODE_COUNT = 0
        TARGET_COUNT = target
        # Initialize emulator 
        mu = Uc(UC_ARCH_X86, UC_MODE_64)

        # map memory
        mu.mem_map(CODE_ADDRESS, 1 * 0x1000) # Code
        mu.mem_map(DATA_ADDRESS, 1 * 0x1000) # DATA
        mu.mem_map(OUTPUT_ADDRESS, 1 * 0x1000) # Output
        mu.mem_map(KEY_ADDRESS, 1 * 0x1000) # KEY
        mu.mem_map(STACK_ADDRESS, 2 * 0x1000) # STACK
        # write machine code to be emulated to memory

        mu.mem_write(CODE_ADDRESS, CODE)
        mu.mem_write(KEY_ADDRESS, key)
        mu.mem_write(DATA_ADDRESS, data)

        # initialize machine registers
        mu.reg_write(UC_X86_REG_RIP, ENTRY_POINT)
        mu.reg_write(UC_X86_REG_RDI, DATA_ADDRESS)
        mu.reg_write(UC_X86_REG_RSI, KEY_ADDRESS)
        mu.reg_write(UC_X86_REG_RDX, OUTPUT_ADDRESS)
        mu.reg_write(UC_X86_REG_RSP, STACK_ADDRESS + 0x1000)

        # tracing all instructions with customized callback
        mu.hook_add(UC_HOOK_CODE, hook_code)

        # emulate machine code in infinite time
        mu.emu_start(ENTRY_POINT, ENTRY_POINT_END)

        result = mu.mem_read(OUTPUT_ADDRESS, 1024)
        print("   [▶️] Result: ",result.hex())

    except UcError as e:
        print("   [💥] BOOM: %s" % e) # https://www.bilibili.com/video/BV1ynKQzHEED



def generateData():
    text = open("text.txt","rb").read() + FLAG + b'\x0A' 
    key = os.urandom(16)
    cipher = ARC4.ARC4Cipher(key).encrypt(text)
    return cipher,key


cipher,key = generateData()
Shocktime = -1
Shocktime=input("time to shock: ")
try:
    Shocktime=int(Shocktime)
except:
    print("wrong input!")
run(cipher,key,Shocktime)

分析：
故障注入攻击，分析题目所给代码，可以发现代码实现了一种比特翻转的漏洞，让Shocktime位置的汇编指令运行过程中所涉及的所有寄存器的最低位的一个字节随机翻转一个bit，这便是shock函数的逻辑。
接下来我们要分析获取FLAG的思路，通过代码

1	`text = open("text.txt","rb").read() + FLAG + b'\x0A'`

我们可以知道明文是由text.txt文件和FLAG拼接成的，使用IDA逆向一下prog文件，可以看到该文件是RC4的加密算法的二进制文件，按理说将Shocktime设为-1就不会执行相关的Shock函数，且RC4是对称密码，连着加密两次按理说会输出原本的密文，然而实际测试结果为：

我们可以发现明文到了parameters.\n之后输出全是0x00，我们再结合题目所给的text.txt文件分析：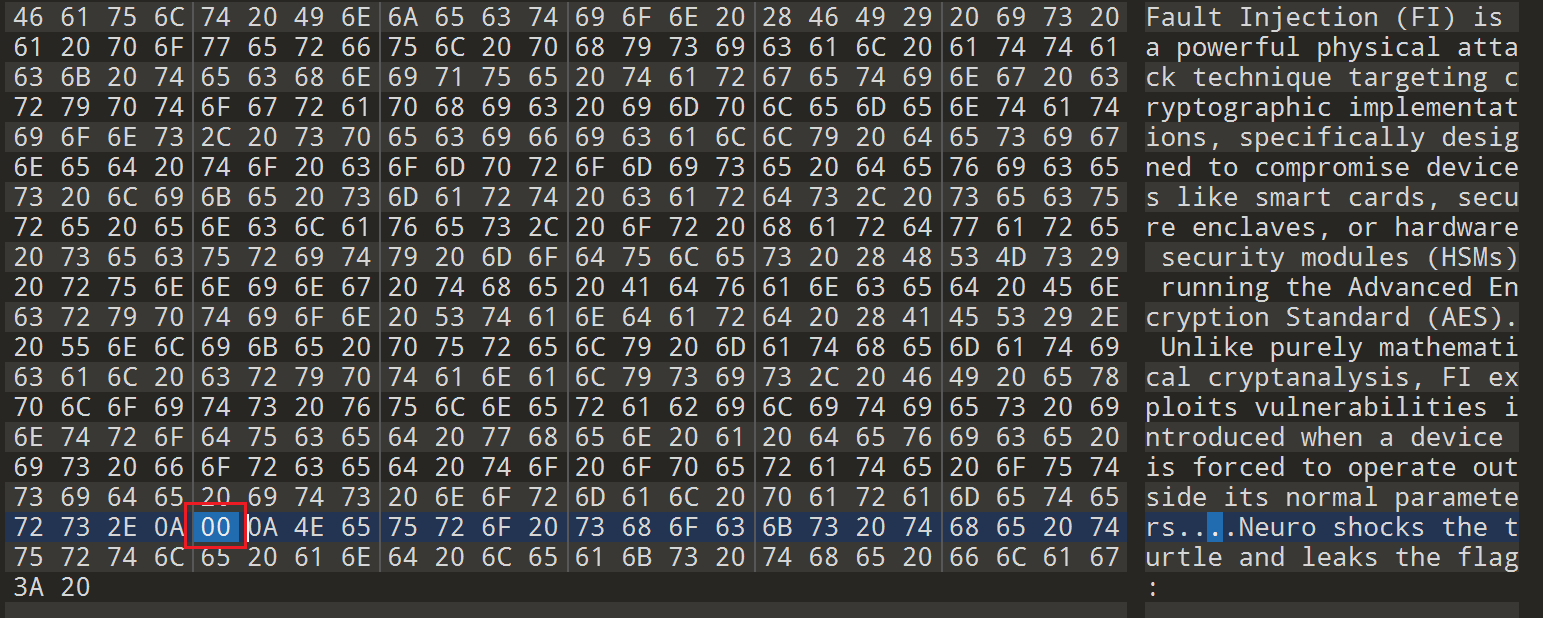

从这个0x00开始就不正常输出了，因此可以合理推测在prog的RC4解密逻辑中对0x00做了特殊的判断。
之后我们的思路就明确了，找到对0x00进行特殊判断的汇编指令，找到该指令执行时对应的CODE_COUNT，再将Shocktime设定为该CODE_COUNT值，通过shock使该指令失效。
通过IDA寻找，可以快速地找到一个十分可疑的指令，它和下边的jnz loc_169结合使用实现了当前eax寄存器值不为0时发生跳转，并且我们可以找到其的相对地址。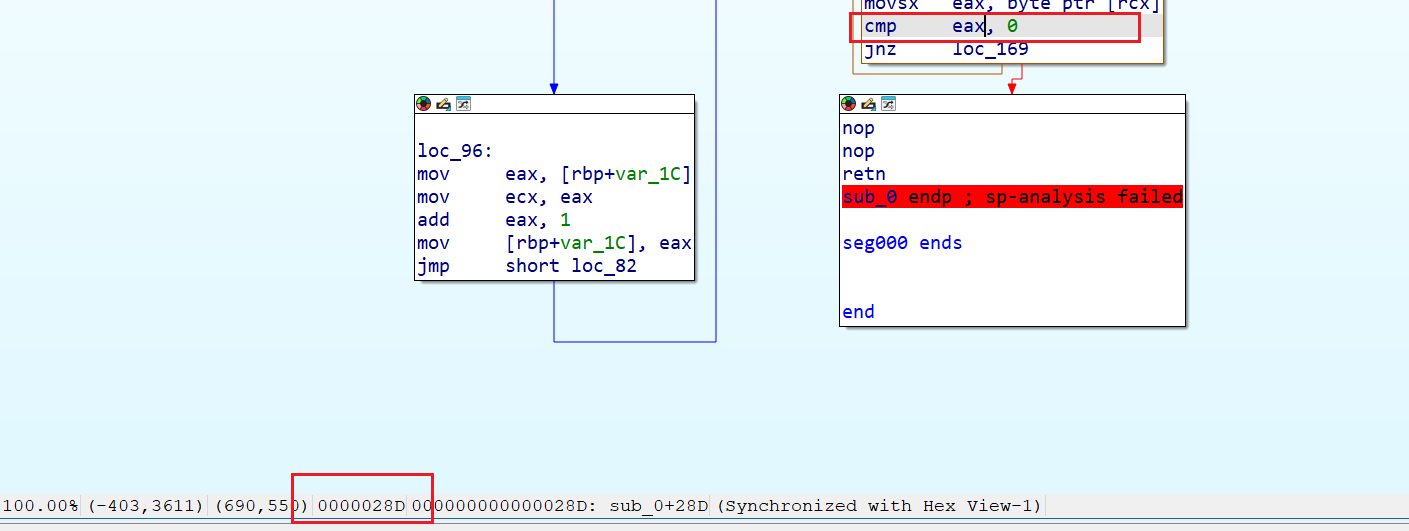

然后我们便能够通过在hook_code中添加下面指令来获取对应的CODE_COUNT：

1 2	`if(address == CODE_ADDRESS + 0x28D): print(CODE_COUNT)`

其中address表示当前指令的地址。将Shocktime设为-1后开始运行题目所给脚本，运行之后可以发现很多输出，由于我们要找到最后解密停止的地方，因此只需要最后一个CODE_COUNT即可。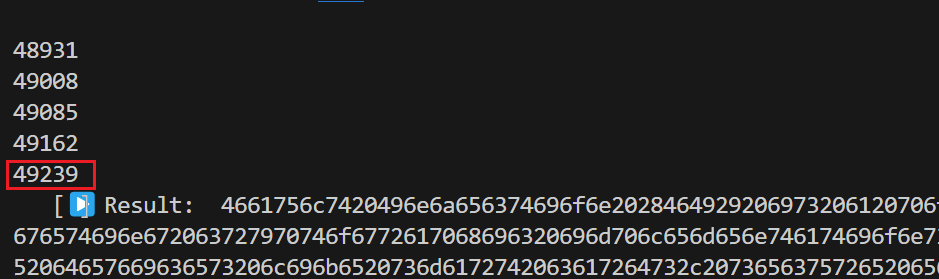

得到对应的CODE_COUNT值为49239，然后连接服务器，设置Shocktime=49239，即可以向对应的汇编指令处进行故障注入，shock函数会在该指令执行前对寄存器进行修改，使对应的eax寄存器的值不再为0，代码会继续向下边进行解密，从而输出flag，脚本如下：

import websocket
import ssl
import re

url = "wss://www.nepctf.com/api/traffic/BVi5vUb4Fp8j0DH8bd3vf?port=9999"

ws = websocket.create_connection(url, sslopt={"cert_reqs": ssl.CERT_NONE})

prompt = ws.recv()
print("Server says:", prompt.decode())

ws.send("49239\n")

shock = ws.recv()
print("Shock:", shock.decode())

hex_line = ws.recv().strip().decode()[12:]
print(hex_line)
plain = bytes.fromhex(hex_line)
print(plain)
if b'NepCTF{' in plain:
    flag = re.search(rb'NepCTF\{[^\}]+\}', plain).group()
    print("Flag:", flag.decode('utf-8', errors='ignore'))

ws.close()

结果如下：

Crypto

NepSign

题目

from gmssl import sm3
from random import SystemRandom
from ast import literal_eval
import os
flag = os.environ["FLAG"]
def SM3(data):
    d = [i for i in data]
    h = sm3.sm3_hash(d)
    return h
def SM3_n(data, n=1, bits=256):
    for _ in range(n):
        data = bytes.fromhex(SM3(data))
    return data.hex()[:bits // 4]


class Nepsign():
    def __init__(self):
        self.n = 256
        self.hex_symbols = '0123456789abcdef'
        self.keygen()

    def keygen(self):
        rng = SystemRandom()
        self.sk = [rng.randbytes(32) for _ in range(48)]
        self.pk = [SM3_n(self.sk[_], 255, self.n) for _ in range(48)] 
        return self.sk, self.pk

    def sign(self, msg, sk=None): 
        sk = sk if sk else self.sk  
        m = SM3(msg) 
        m_bin = bin(int(m, 16))[2:].zfill(256) 
        a = [int(m_bin[8 * i: 8 * i + 8], 2) for i in range(self.n // 8)]
        step = [0] * 48;
        qq = [0] * 48 
        for i in range(32):
            step[i] = a[i] 
            qq[i] = SM3_n(sk[i], step[i])
        sum = [0] * 16
        for i in range(16):
            sum[i] = 0
            for j in range(1, 65):
                if m[j - 1] == self.hex_symbols[i]:
                    sum[i] += j
            step[i + 32] = sum[i] % 255
            qq[i + 32] = SM3_n(sk[i + 32], step[i + 32]) 
        return [i for i in qq]

    def verify(self, msg, qq, pk=None):
        qq = [bytes.fromhex(i) for i in qq]
        pk = pk if pk else self.pk
        m = SM3(msg)
        m_bin = bin(int(m, 16))[2:].zfill(256)
        a = [int(m_bin[8 * i: 8 * i + 8], 2) for i in range(self.n // 8)]
        step = [0] * 48;
        pk_ = [0] * 48
        for i in range(32):
            step[i] = a[i]
            pk_[i] = SM3_n(qq[i], 255 - step[i])
        sum = [0] * 16
        for i in range(16):
            sum[i] = 0
            for j in range(1, 65):
                if m[j - 1] == self.hex_symbols[i]:
                    sum[i] += j
            step[i + 32] = sum[i] % 255
            pk_[i + 32] = SM3_n(qq[i + 32], 255 - step[i + 32]) 
        return True if pk_ == pk else False


print('initializing...')
Sign = Nepsign()
while 1:
    match int(input('> ')):
        case 1:
            msg = bytes.fromhex(input('msg: ')) 
            if msg != b'happy for NepCTF 2025': 
                print(Sign.sign(msg))
            else:
                print("You can't do that")
        case 2:
            qq = literal_eval(input('give me a qq: '))
            if Sign.verify(b'happy for NepCTF 2025', qq): 
                print(flag)

分析

首先明确我们的目的，是要求出一个长度为48的qq列表，这个qq列表中的qq[i]都是sk[i]经过step[i]次SM3哈希之后得到的值。
关键点分析：

由于我们已经知道了明文就是happy for NepCTF 2025，因此根据题目给出的算法我们能够求出step列表
其次，我们可以无限次地请求签名
最重要的一点是，我们可以手动对qq[i]进行step[i]的增加，因为我们知道SM3的算法
因此，我们的思路已经明确，就是要找到一个qq序列，保证对应每个step[i]都小于原本明文的step[i]，这样我们就可以计算出target_step[i]-step[i]，从而手动恢复出正确的qq序列。
注意，我们并不需要这48个qq[i]由同一次签名得出，因为每个qq[i]和step[i]的对应关系跟其他的没有联系，也就是说，我们可以重复请求签名，知道每个i都有了对应的qq[i]、step[i]使得step[i]<target_step[i]。

解答


from pwn import *
from gmssl import sm3
import os, ast, random, sys

context.log_level = 'info'   

HEX = '0123456789abcdef'

def SM3(data: bytes) -> str:
    return sm3.sm3_hash([b for b in data])

def SM3_n(data: bytes, n: int) -> str:
    for _ in range(n):
        data = bytes.fromhex(SM3(data))
    return data.hex()[:64]

def calc_steps(msg: bytes):
    m_hex = SM3(msg)
    m_bin = bin(int(m_hex, 16))[2:].zfill(256)
    steps = [0]*48

    # 前 32 个直接取 256bit 哈希的各字节
    for i in range(32):
        steps[i] = int(m_bin[8*i:8*i+8], 2)

    # 后 16 个按出现位置求和再 mod 255
    for i in range(16):
        s = 0
        for j, ch in enumerate(m_hex, 1):
            if ch == HEX[i]:
                s += j
        steps[32+i] = s % 255
    return steps

TARGET_MSG = b'happy for NepCTF 2025'
target_step = calc_steps(TARGET_MSG)

HOST, PORT = 'nepctf30-yctq-jzxl-h59c-3yzhv08pk172.nepctf.com',443 
io = remote(HOST, PORT , ssl = True)
io.recvuntil(b'initializing') 

collected_q  = [None]*48
collected_st = [None]*48
need = set(range(48))



log.info('[*] Start collecting chain values …')

while need:

    io.sendlineafter(b'> ', b'1')
    rnd_msg = os.urandom(16)
    io.sendlineafter(b'msg: ', rnd_msg.hex().encode())

    sig_line = io.recvline().strip().decode()
    try:
        sig_list = ast.literal_eval(sig_line)
        assert isinstance(sig_list, list) and len(sig_list) == 48
    except Exception as e:
        log.error(f'parse sign fail: {e}')
        sys.exit(1)

    cur_step = calc_steps(rnd_msg)

    updated = False
    for i in list(need): 
        if cur_step[i] <= target_step[i]:
            collected_q[i]  = sig_list[i]
            collected_st[i] = cur_step[i]
            need.remove(i)
            updated = True
    if updated:
        log.info(f'   progress: {48-len(need)}/48 collected')

log.success('[+] All indices satisfied, forging final signature …')

final_qq = []
for i in range(48):
    delta = target_step[i] - collected_st[i]
    q_hex = collected_q[i]
    if delta:
        q_hex = SM3_n(bytes.fromhex(q_hex), delta)
    final_qq.append(q_hex)

log.info(f'Final qq: {final_qq}')
io.sendlineafter(b'> ', b'2')
io.sendlineafter(b'give me a qq: ', str(final_qq).encode())

flag = io.recvline_contains(b'NepCTF').decode(errors='ignore')
print(f'\n{flag}')

LatticeBros

题目

#已知α的极小多项式为三次多项式f(x),即f(α)=0,且α≈54236.606188881754809671280151541781895183337725393
#上述极小多项式的常数项为a0

from secret import a0,alpha
import gmpy2
from Crypto.Util.number import long_to_bytes
import random
from math import sqrt,log2

d=981020902672546902438782010902608140583199504862558032616415
p = d - a0

k=sqrt(log2(p))+log2(log2(p))
B = 2**30
assert B < p/2**k

m = 30
assert m > 2*sqrt(log2(p))

samples = []
betas = []

f = open("samples.txt",'w')
for _ in range(m):
    t = random.randint(1, p-1)
    beta = random.randint(-B + 1, B - 1)
    a = (t * alpha - beta) % p
    samples.append((t, a))
    betas.append(beta)

f.write(str(samples))

for i in range(0,30):
    assert (betas[i]-samples[i][0]*alpha+samples[i][1])%p == 0

#flag = long_to_bytes(alpha)

分析

已知$\alpha$的极小多项式是三次多项式，且$f(\alpha)=0$，即
$\alpha^3 + a_2\alpha^2 + a_1\alpha +a_0=0$

可以构造格：

$$ (1,a_2,a_1,a_0) \begin{pmatrix} 1 & 0 & 0 & \alpha^{3} C \\ 0 & 1 & 0 & \alpha^{2} C \\ 0 & 0 & 1 & \alpha C \\ 0 & 0 & 0 & C \end{pmatrix} \\ =(1,a_2,a_1,\epsilon C) $$

其中$\epsilon$接近0，则$\epsilon C$接近0。格基规约就可以求出$a_2、a_1$，然后带回方程式求出$a_0$，之后就是正常的HNP问题。

解答

from Crypto.Util.number import *
import ast

with open('samples.txt', 'r') as f:
    samples_str = f.read()
    samples = ast.literal_eval(samples_str)

d = 981020902672546902438782010902608140583199504862558032616415
alpha = 54236.606188881754809671280151541781895183337725393
for i in range(100):
    C = 2^i
    M = matrix(QQ,[[1,0,0,C*alpha^3],[0,1,0,C*alpha^2],[0,0,1,C*alpha],[0,0,0,C]])

    L = M.LLL()
    for l in L:
        if abs(l[0]) == 1:
            r = l
            break
    #print(r)
    a1 = r[2]
    a2 = r[1]
    a0 = int(-alpha^3 - a2*alpha^2 - a1*alpha)
    p = d - a0
    #print(p)

    a_list = []
    t_list = []
    for t, a in samples:
        a_list.append(a)
        t_list.append(t)
    n = len(t_list)

    kbits = 30
    K = 2 ^ kbits -1
    #print(t_list)
    M = Matrix(QQ,n+2,n+2)
    for i in range(n):
        M[i,i] = p
        M[-2,i] = t_list[i]
        M[-1,i] = -a_list[i]
    b = K/p
    M[-2,-2] = b
    M[-1,-1] = K
    #print(M)
    L2 = M.LLL()
    x = L2[1][-2] // b % p
    ans = long_to_bytes(x)
    if b'NepCTF{' in ans:
        print(i)
        print(ans)
        break

ezrsa2

题目

from Crypto.Util.number import getStrongPrime, getRandomNBitInteger, GCD, inverse, long_to_bytes, bytes_to_long, sieve_base
from flag import flag


def gen_parameters(gamma=0.33, beta=0.33):
    p = getStrongPrime(1024)
    q = getStrongPrime(1024)
    N = p*q
    phi = (p-1)*(q-1)
    while True:
        d = getRandomNBitInteger(int(2048*beta))
        if GCD(d, phi) == 1:
            break
    e = inverse(d, phi)
    
    hints = []
    M = 1
    for i in range(1, len(sieve_base)):
        li = sieve_base[i]  #素数
        hints.append(d%li)
        M *= li
        if M.bit_length() >= 1024*gamma:
            break
    
    return e, N, hints



def main():
    e,N,hints = gen_parameters()
    print(f'e={hex(e)}')
    print(f'N={hex(N)}\n')
    print(f'hints={hints}\n')
    
    flag_prefix = b'NepCTF{'
    assert flag.startswith(flag_prefix)
    assert flag.endswith(b'}')
    
    pt = bytes_to_long(flag[len(flag_prefix):-1])
    ct = pow(pt, e, N)
    print(f'ct={hex(ct)}')
    
main()


"""
e=0x73915608ed64c9cf1a2279684cab4f4a78fba229d45d4f860971a241481363470a19cb0dc0d00f816b5befdaca017cf71483e96ef17b36179012f5194a0e6bf481bb06c2644f74c6812efb65d05c00631f282d6aa55c0bc140a1830b95a1cf4b6024cb0db53f2c2189897c41f22e2eec773723f531ec4bfa537fae6de5fe480cf46fe17850f7eb47df08194d95db3d26ac923b26e110ee645239ab586bbc546ddc5906f280a106edbb727ccb05536b5a3f5c0ebcf865c95ce58be54f7f3547aa53baa218b0dfa98e42d925fa341e45f94a3b16b0c83802660c7f34de3336cb21f219073cf8e9f5e39d47f0a9a9ee7c255f09a6add9a2f7a47960f4a853183d29
N=0xba8956e81394f3f1265ca5d9c4ad1ab0078bb43c4b80a231ab2cc62246ae45f66a562252622aed2cbbfc08647ef2fec0f97a632bf2242845f4b3af0c427cec3d90f42e90278a5a0feeed0922a8cd2278074ac54e9cfc0e96ff68f8d8f266dd87dc1cc59c2895ec884de2022311767f6a9a7e0bd288c79620e28b83bb3c8d8ad1047c839d6ccf5544eaf434a5f00b951769ab3121298d04b63a162757beb3d49917cd0c9e02ee1ac29398c8130961d5a2f2833aba1e538edb7bb97071f40fae543d1622f0c9206c6d4d8abb2ac1b93ebfb603c2f3a909ede357ade4043550fe540d13a4e87db8d731fe130f15a43a1a00364f5da2d87f7b660c3a04e734218a11

hints=[1, 3, 0, 3, 9, 16, 10, 14, 5, 11, 21, 18, 30, 30, 38, 2, 20, 62, 66, 1, 22, 56, 41, 13, 78, 59, 51, 6, 57, 117, 73, 75, 96, 112, 50, 93, 158, 97, 146, 8, 65, 96, 186, 161, 90, 131, 46, 32, 140, 133, 50, 43, 151, 234]

ct=0x101b284ad196b5bbd3d3df00a7d3577caeb29c681bdd122582b705afc671febf45d4f3786640e55aadd6a31ecc49175f97b772720f1735f8555f768b137a4643cd6958f80a3dfca4d0270ad463d6dde93429940bd2abb5ad8408b0906fa8d776544a1c50cc0d95939bef4c3fb64d0b52dca81ff0f244fc265bfc0bc147435d05f8f1a146e963a1403b3c123b4d6e73d1fd897109995009be1673212607f0ea7ae33d23f3158448b05c28ea6636382eee9436c4a6c09023ead7182ecd55ac73a68d458d726e1abc208810468591e63f4b4c2c1f3ce27c4800b52f7421ccab432c03e88b3b255740d719e40e0226eabb7633d97ed210e32071e2ac36ed17ef442e
"""

分析

题中给出了$d$的生成算法，我们可以知道$d\approx N^{0.33}$，和我们熟知的Boneh and Durfee attack的攻击上限$N^{0.292}$还有些差距，但是$hints$的暴露使得我们能够利用中国剩余定理求出$d$的部分低位$d_l$，可以表示为$d=d_hM+d_l$
因为我们已知了部分低位，因此我们的思路尽量往coppersmith上边靠，由于泄露的是$d_l$，我们选的的多项式为：$ed=1+k\phi$
稍微调整一下，
$e(d_hM+d_l)=1+k(N-p-q+1)$
=>$d_heM = 1+k(N-p-q+1)-ed_l$
两边同时模上$eM$，得$0\equiv 1+k(N-p-q+1)-ed_l \mod eM$
设$x=k，y=p+q$得$f(x,y)\equiv 1+x(N-y+1)-ed_l \mod eM$
并且我们可以算出$x\approx 2^{680}，y\approx 2^{1024}$然后直接打二元coppersmith即可

解答

from Crypto.Util.number import *

import gmpy2
import itertools
e=0x73915608ed64c9cf1a2279684cab4f4a78fba229d45d4f860971a241481363470a19cb0dc0d00f816b5befdaca017cf71483e96ef17b36179012f5194a0e6bf481bb06c2644f74c6812efb65d05c00631f282d6aa55c0bc140a1830b95a1cf4b6024cb0db53f2c2189897c41f22e2eec773723f531ec4bfa537fae6de5fe480cf46fe17850f7eb47df08194d95db3d26ac923b26e110ee645239ab586bbc546ddc5906f280a106edbb727ccb05536b5a3f5c0ebcf865c95ce58be54f7f3547aa53baa218b0dfa98e42d925fa341e45f94a3b16b0c83802660c7f34de3336cb21f219073cf8e9f5e39d47f0a9a9ee7c255f09a6add9a2f7a47960f4a853183d29
N=0xba8956e81394f3f1265ca5d9c4ad1ab0078bb43c4b80a231ab2cc62246ae45f66a562252622aed2cbbfc08647ef2fec0f97a632bf2242845f4b3af0c427cec3d90f42e90278a5a0feeed0922a8cd2278074ac54e9cfc0e96ff68f8d8f266dd87dc1cc59c2895ec884de2022311767f6a9a7e0bd288c79620e28b83bb3c8d8ad1047c839d6ccf5544eaf434a5f00b951769ab3121298d04b63a162757beb3d49917cd0c9e02ee1ac29398c8130961d5a2f2833aba1e538edb7bb97071f40fae543d1622f0c9206c6d4d8abb2ac1b93ebfb603c2f3a909ede357ade4043550fe540d13a4e87db8d731fe130f15a43a1a00364f5da2d87f7b660c3a04e734218a11

hints=[1, 3, 0, 3, 9, 16, 10, 14, 5, 11, 21, 18, 30, 30, 38, 2, 20, 62, 66, 1, 22, 56, 41, 13, 78, 59, 51, 6, 57, 117, 73, 75, 96, 112, 50, 93, 158, 97, 146, 8, 65, 96, 186, 161, 90, 131, 46, 32, 140, 133, 50, 43, 151, 234]

ct=0x101b284ad196b5bbd3d3df00a7d3577caeb29c681bdd122582b705afc671febf45d4f3786640e55aadd6a31ecc49175f97b772720f1735f8555f768b137a4643cd6958f80a3dfca4d0270ad463d6dde93429940bd2abb5ad8408b0906fa8d776544a1c50cc0d95939bef4c3fb64d0b52dca81ff0f244fc265bfc0bc147435d05f8f1a146e963a1403b3c123b4d6e73d1fd897109995009be1673212607f0ea7ae33d23f3158448b05c28ea6636382eee9436c4a6c09023ead7182ecd55ac73a68d458d726e1abc208810468591e63f4b4c2c1f3ce27c4800b52f7421ccab432c03e88b3b255740d719e40e0226eabb7633d97ed210e32071e2ac36ed17ef442e

m_list = []
for i in range(1,len(hints)+1):
    m_list.append(sieve_base[i])
M = prod(m_list)
dl = crt(hints,m_list)%M
#print(dl)
#print(M)

def small_roots(f, bounds, m=1, d=None):
    if not d:
        d = f.degree()
        print(d)
    R = f.base_ring()
    N = R.cardinality()
    #f /= f.coefficients().pop(0)
    f = f.change_ring(ZZ)
    G = Sequence([], f.parent())
    for i in range(m + 1):
        base = N ^ (m - i) * f ^ i
        for shifts in itertools.product(range(d), repeat=f.nvariables()):
            g = base * prod(map(power, f.variables(), shifts))
            G.append(g)
    B, monomials = G.coefficient_matrix()
    monomials = vector(monomials)
    factors = [monomial(*bounds) for monomial in monomials]
    for i, factor in enumerate(factors):
        B.rescale_col(i, factor)
    B = B.dense_matrix().LLL()
    B = B.change_ring(QQ)
    for i, factor in enumerate(factors):
        B.rescale_col(i, 1 / factor)
    H = Sequence([], f.parent().change_ring(QQ))
    for h in filter(None, B * monomials):
        H.append(h)
        I = H.ideal()
        if I.dimension() == -1:
            H.pop()
        elif I.dimension() == 0:
            roots = []
            for root in I.variety(ring=ZZ):
                root = tuple(R(root[var]) for var in f.variables())
                roots.append(root)
            return roots
    return []

R.<x,y> = PolynomialRing(Zmod(e*M))
f = 1+x*(N-y+1)-e*dl
X = 2^680
Y = 2^1024
k,p_q = small_roots(f,(X,Y),2,4)[0]   #求不出时调整m，d的参数值
k,p_q = int(k),int(p_q)
phi = N - p_q +1
d = inverse(e,phi)
m = pow(ct,d,N)
ans = long_to_bytes(m).decode()
print(f"NepCTF{{{ans}}}")
#NepCTF{larg3r_M0du1u5_1nf0_g1ves_b3773r_b0und5}

unloopshock

题目

from unicorn import *
from unicorn.x86_const import *
from capstone import *
from capstone.x86_const import *
import os
import sys
import random
from Crypto.Util.number import *

flag = os.getenv('FLAG','test{This_is_a_test_flag_connect_to_get_true_flag}').encode()


CODE_COUNT = 0
TARGET_COUNT = 0
# memory address where emulation starts
CODE_ADDRESS    = 0x110000
DATA_ADDRESS    = 0x220000
KEY_ADDRESS     = 0x440000
STACK_ADDRESS   = 0x880000
CODE = b''
with open("./src/prog_aes4","rb") as f:
    CODE = f.read()


ENTRY_POINT = CODE_ADDRESS + 0x9E5
ENTRY_POINT_END = CODE_ADDRESS + 0xF6F


def flipBit(uc:Uc,reg_name:str):
    randBit = random.randint(0,7) #not 0,63
    reg_num = eval("UC_X86_REG_" + reg_name.upper())
    reg_value = uc.reg_read(reg_num)
    reg_value ^= 1 << randBit
    uc.reg_write(reg_num,reg_value)

def shock(uc:Uc):
    rip = uc.reg_read(UC_X86_REG_RIP)
    code = uc.mem_read(rip,16)
    md = Cs(CS_ARCH_X86, CS_MODE_64)
    md.detail = True
    dis = None
    for d in md.disasm(code, 0):
        dis = d
        break
    for reg_list in dis.regs_access():
        for reg in reg_list:
            flipBit(uc,md.reg_name(reg))


def hook_code(uc:Uc, address, size, user_data):
    global CODE_COUNT
    if(CODE_COUNT >= 2000000):
        print("   [⏰] Time Limit Exceed")
        uc.emu_stop()
    if(CODE_COUNT == TARGET_COUNT):
        print("   [⚡] Shock!")
        shock(uc)
    CODE_COUNT += 1

def run(data,key,target):
    print("   [🔒] to enc: ",data.hex())
    try:
        global CODE_COUNT
        global TARGET_COUNT
        CODE_COUNT = 0
        TARGET_COUNT = target
        # Initialize emulator 
        mu = Uc(UC_ARCH_X86, UC_MODE_64)

        # map memory
        mu.mem_map(CODE_ADDRESS, 2 * 0x1000) # Code
        mu.mem_map(DATA_ADDRESS, 1 * 0x1000) # DATA
        mu.mem_map(KEY_ADDRESS, 1 * 0x1000) # KEY
        mu.mem_map(STACK_ADDRESS, 2 * 0x1000) # STACK
        # write machine code to be emulated to memory

        mu.mem_write(CODE_ADDRESS, CODE)
        mu.mem_write(KEY_ADDRESS, key)
        mu.mem_write(DATA_ADDRESS, data)

        # initialize machine registers
        mu.reg_write(UC_X86_REG_RIP, ENTRY_POINT)
        mu.reg_write(UC_X86_REG_RDI, DATA_ADDRESS)
        mu.reg_write(UC_X86_REG_RSI, 16)
        mu.reg_write(UC_X86_REG_RDX, KEY_ADDRESS)
        mu.reg_write(UC_X86_REG_RSP, STACK_ADDRESS + 0x1000)

        # tracing all instructions with customized callback
        mu.hook_add(UC_HOOK_CODE, hook_code)

        # emulate machine code in infinite time
        mu.emu_start(ENTRY_POINT, ENTRY_POINT_END)

        result = mu.mem_read(DATA_ADDRESS, 16)
        print("   [▶️] Result: ",result.hex())

    except UcError as e:
        print("   [💥] BOOM: %s" % e) # https://www.bilibili.com/video/BV1ynKQzHEED
    return


AES_KEY = os.urandom(16)
AES_PTS = b''
Shocktime = 9999999

if __name__ == '__main__':
    count=0
    while count < 1:
        count += 1
        print("Round %d / 1"%(count))
        print("Input your data: in hex(max 16 bytes)")
        try:
            AES_PTS = bytes.fromhex(input())[0:16]
        except:
            print("wrong input!")
            sys.exit(1)
        Shocktime=input("time to shock: ")
        try:
            Shocktime=int(Shocktime)
        except:
            print("wrong input!")
            sys.exit(1)
        run(AES_PTS,AES_KEY,Shocktime)    
        guesskey=input("now give me your guess key: ")
        if guesskey[0] == "n":
            continue
        try:
            guesskey=bytes.fromhex(guesskey)[0:16]
        except:
            print("wrong input!")
            sys.exit(1)
        if guesskey==AES_KEY:
            print("FLAG:",flag)
            sys.exit(0)
        else:
            print("No Second Chance")
            sys.exit(1)

分析

故障注入攻击，分析题目，跟MISC中的easyshock比较相似，其中的shock逻辑是一样的，这一题的交互逻辑和题目都在提示我们跟密钥泄露有关，只要求出key我们就能得到FLAG。
使用IDA逆向一下progaes4，发现是AES加密算法，逐个分析函数之后，发现函数sub_1BC控制着密钥扩展逻辑，根据我们了解的AES相关知识可以知道，扩展密钥由十一组组成，每组由4个4字节组成，其中第一组就是原始密钥。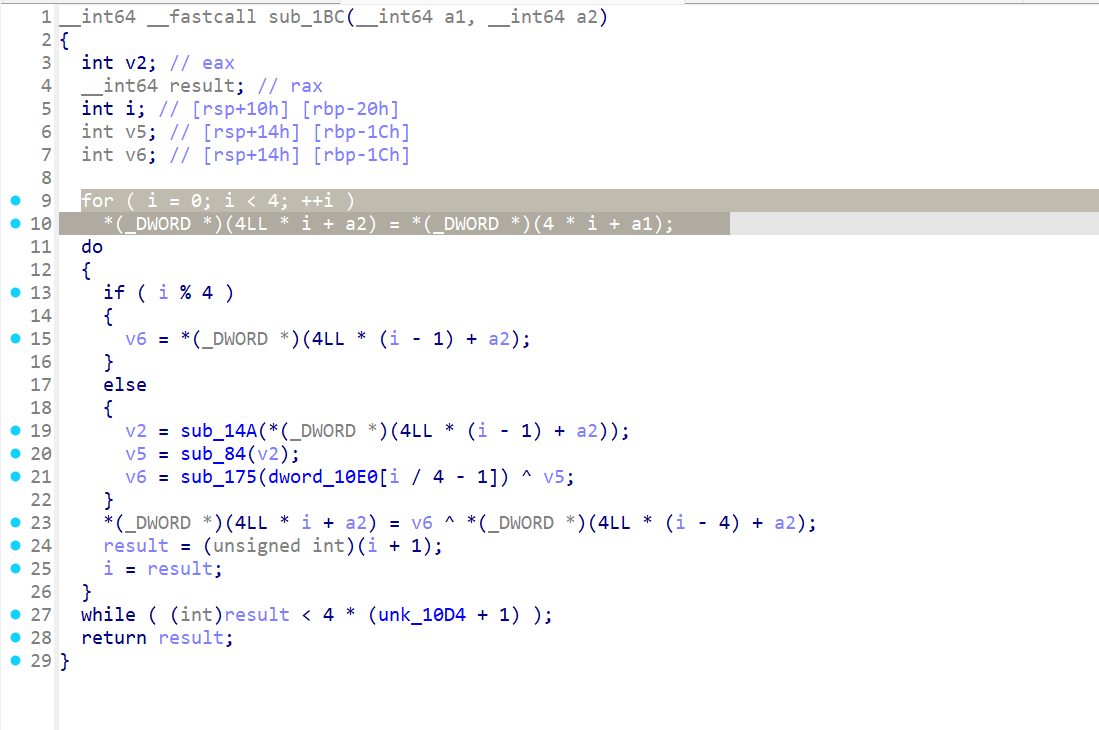

由于我们可以自定义加密明文，也就是说，我们的目的就是通过修改密钥扩展算法，再结合明文和密钥的关系来获取密钥。通过分析我们可以通过修改i的大小，让i直接跳过do-while，这样扩展密钥就会变成除了第一组是原始密钥key，其他10组都默认为0，这样的话我们就能用来生成扩展密钥为全0进行解密，最后再异或一下明文m就能得到key。
首先我们要找到对应的注入点，通过查看该函数的汇编指令，找到扩展密钥初始化时++i的指令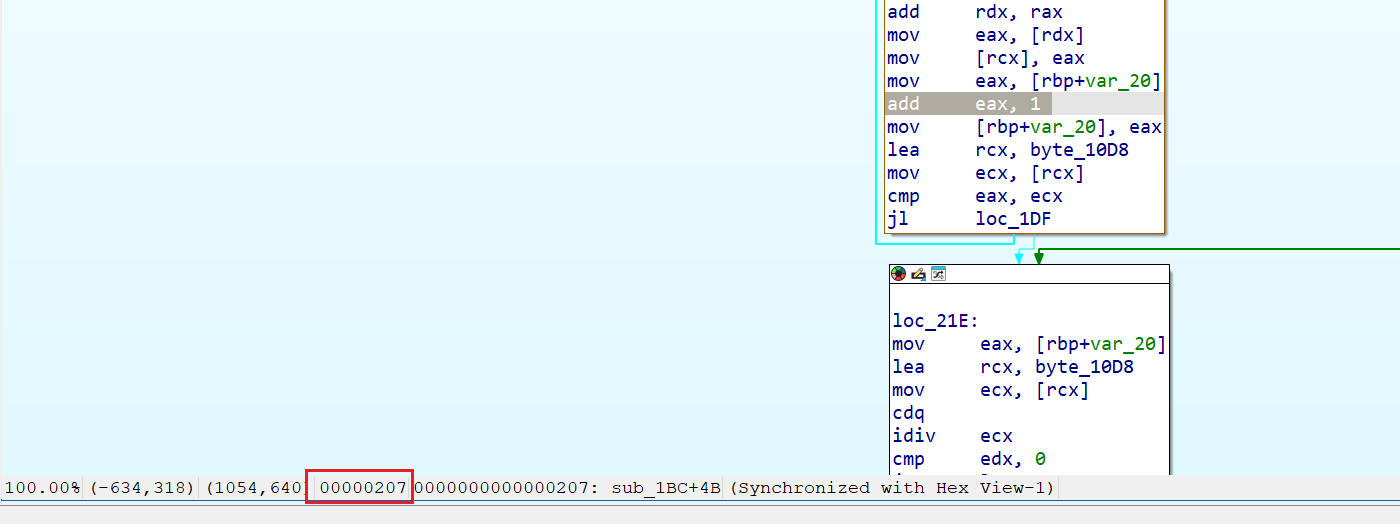

找到相对地址为0x207，然后在hook_code中添加以下代码来获取对应的故障注入点：

1 2	`if(address == CODE_ADDRESS + 0x207): print(CODE_COUNT)`

运行题目所给脚本，取最后一个CODE_COUNT作为Shocktime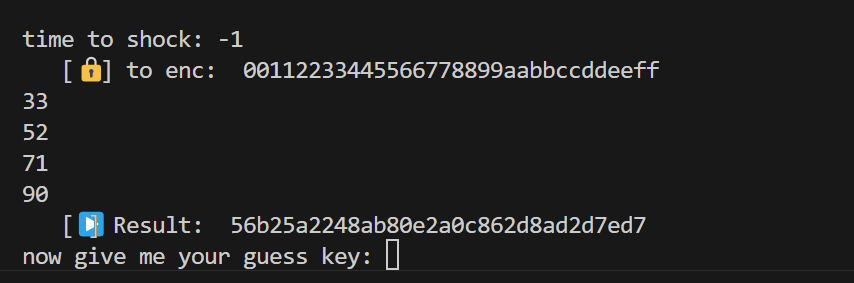

得到Shocktime为90，之后便可以进行注入了，首先我们要有一个能够自定义轮密钥的AES解密脚本，在网上随便找了一个：AES 加解密 python手动实现 - wuuconix’s blog
稍微对脚本进行修改，写一个生成全0的轮密钥生成函数，并将解密的输出结果调整一下即可。

解答

aes.py：

import copy
from Crypto.Util.number import *

def mul(poly1, poly2):   # 两个多项式相乘
	result = 0  
	for index in range(poly2.bit_length()):
		if poly2 & (1 << index):
			result ^= (poly1 << index)
	return result

def mod(poly, mod = 0b100011011):    # 多项式poly模多项式100011011
	while poly.bit_length() > 8:  
		poly ^= (mod << (poly.bit_length() - 9))
	return poly

def substitute(m_hex, inverse=False):
    m_s = []
    box = s_box if not inverse else i_s_box
    for i in m_hex:
        x, y = int(i, 16) // 16, int(i, 16) % 16
        temp = hex(box[x*16+y])
        m_s.append(temp)
    return m_s

s_box =   [0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76, 0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0, 0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15, 0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75, 0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84, 0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF, 0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8, 0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2, 0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73, 0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB, 0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79, 0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08, 0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A, 0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E, 0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF, 0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16]
i_s_box = [0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB, 0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB, 0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E, 0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25, 0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92, 0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84, 0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06, 0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B, 0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73, 0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E, 0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B, 0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4, 0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F, 0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF, 0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61, 0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D]
rcon = [0x1, 0x2, 0x4, 0x8, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36]
mix_column_matrix   = [0x2, 0x3, 0x1, 0x1, 0x1, 0x2, 0x3, 0x1, 0x1, 0x1, 0x2, 0x3, 0x3, 0x1, 0x1, 0x2] # 列混合乘的矩阵
i_mix_column_matrix = [0xe, 0xb, 0xd, 0x9, 0x9, 0xe, 0xb, 0xd, 0xd, 0x9, 0xe, 0xb, 0xb, 0xd, 0x9, 0xe] # 列混合乘的逆矩阵

def xor(a, key): #a和key都是列表，都存了16字节
    return [hex(int(a[i], 16) ^ int(key[i], 16)) for i in range(0, 16)]

def get_hex(s): #得到一个字符串的十六进制值，以列表形式返回
    return [hex(ord(i)) for i in s]

def shiftrows(a, inverse=False): #inverse为True时表示为逆操作，默认为False
    return [ a[0], a[5], a[10], a[15], a[4], a[9], a[14], a[3], a[8], a[13], a[2], a[7], a[12], a[1], a[6], a[11] ] if not inverse else [ a[0], a[13], a[10], a[7], a[4], a[1], a[14], a[11], a[8], a[5], a[2], a[15], a[12], a[9], a[6], a[3] ]

def mixcolumn(m_row, inverse=False):
    matrix = mix_column_matrix if not inverse else i_mix_column_matrix
    m_col = []
    for i in range(0, 16):
        x, y = i % 4, i // 4 
        result = 0
        for j in range(0, 4):
            result ^= (mul(matrix[x * 4 + j], int(m_row[y * 4 + j], 16)))
        result = mod(result)
        m_col.append(hex(result))
    return m_col

def key_zero_rotate():
    key_rotate = [['0x00' for _ in range(16)] for _ in range(11)]
    return key_rotate

def aes_decrypt(c, key_rotate):
    c_hex = ['0x' + c[i * 2] + c[i * 2 + 1] for i in range(0, 16)] #将密文恢复为列表
    c_xor = xor(c_hex, key_rotate[10])
    c_row = shiftrows(c_xor, inverse=True)
    c_s = substitute(c_row, inverse=True)
    for rotate in range(9, 0, -1): #循环9次
        c_xor = xor(c_s, key_rotate[rotate])
        c_col = mixcolumn(c_xor, inverse=True)
        c_row = shiftrows(c_col, inverse=True)
        c_s = substitute(c_row, inverse=True)
    plain_bytes = bytes(int(x, 16) for x in xor(c_s, key_rotate[0]))
    return plain_bytes.hex()

破解脚本ans.py：

import websocket
import ssl
import re
import aes
from Crypto.Util.number import *


url = "wss://www.nepctf.com/api/traffic/Cb0Tcf4XIXmHG8dG1tqVI?port=9999"
ws = websocket.create_connection(url, sslopt={"cert_reqs": ssl.CERT_NONE})

prompt = ws.recv()
print("Server says:", prompt.decode())

plaintext = "00112233445566778899aabbccddeeff"
ws.send(plaintext+"\n")
msg = ws.recv()
print("msg=",msg)
ws.send("90\n")

shock = ws.recv()
print("msg1=",shock.decode())
msg2 = ws.recv()
print("msg2=",msg2)
msg3 = ws.recv().decode()
print("msg3=",msg3)
cipher = re.search(r'([0-9a-fA-F]{32})', msg3).group(1)
print("cipher=",cipher)

#使用纯0轮密钥解密
rotate_key = aes.key_zero_rotate()
plain = aes.aes_decrypt(cipher,rotate_key)

key = hex(int(plaintext,16) ^ int(plain,16))[2:]
print("key=",key)
ws.send(key+"\n")
msg4 = ws.recv().decode()
print(msg4)

ws.close()

运行获取FLAG，提示一下，由于我们的故障注入并不能保证比特翻转后的i一定大于44，因此需要多尝试几次才能获得flag。

Study

#CTF

NepCTF 2025 Writeup

http://ramoor.github.io/2025/07/25/NepCTF 2025 Writeup/

作者

Ramoor

发布于

2025年7月25日

许可协议

AFCTF 2018 Writeup 上一篇

羊城杯 2023 Wp（复现）下一篇